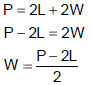Solving Problems With Formulas
Evaluating Formulas
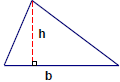
A formula describes a known relationship among quantities. For
example, the formula A=½ bh relates the area A of a
triangle to
the length so fits base b and height h.
If A=20ft2 and b=5ft,what is the value of h?
 |
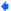 Substitute the values for
A and b. |
| Clear the fraction. |
|
| Solve the equation for
h. |
|
Solving Formulas
The formula A=½bh is solved for A because
A is alone on
one side
of the formula. We can solve the formula for b or h by applying the
same strategy we use to solve an equation.
To solve the formula for h, first we clear the fraction:
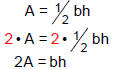
Next, we divide both sides by b to get h alone on one side:
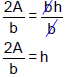
Comparing Equations and Formulas
| Equation Solve: 42 = 2x + 10 To solve the equation for x, we
|
Formula Solve the formula for x: y = mx + b To solve the formula for x, we
|
Solving Problems With Formulas
To evaluate a formula, substitute the given value(s) for
the
variable(s) and solve for the unknown variable.
To solve a formula for a specified variable,
1.Clear fractions and decimals if necessary.
2.Remove parentheses.
3.Combine like terms on the same side.
4.Add opposites to get the specified variable alone on one side
of the formula.
5.Multiply or divide to solve for the specified variable
Example 1(a) and (b)
| a) Write a formula for the perimeter of a rectangle. Use L for the length, W for the width and P for the perimeter.
P = 2L + 2W |
b) Use the formula to find the perimeter of a rectangular pool that has a length of 24 feet and a width of 16feet
P = 80 feet |
.Example 1(c) and (d)
| c) A rectangular car lot has a perimeter of 60 meters. Find the length of the lot when the width measures 12 meters.
L = 18 meters |
d) Solve the formula P = 2L + 2W for W. Solution:
|
Example 2
The length of an oil painting is 4 meters longer than
twice its width.
If the perimeter of the painting is 56 meters, find the length.
Read the problem:
Given:
Perimeter = 56 meters
Length=2·(width)+4
Unknown: Width
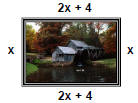
Assign a variable: Width=x
Translate: Length=2x+4
Equation: Use the formula to write the equation:
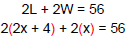
Solve the equation:
2(2x+4)+2(x)=56
4x+8+2x=56
6x+8=56
6x=48
x=8
State the answer:
Width = x = 8 meters
Length = 2(8) + 4 = 20 meters
Practice Exercise 1
Substitute the given values into the formula and solve for
the
unknown variable.
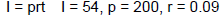
A. t = 9.72
B. t = 97.2
C. t = 0.3
D. t = 3 
Practice Exercise 2
Ted drove to his grand parents' house for a holiday
weekend. The
total distance (one way) was 216 miles. If the trip took 8 hours,
how fast was he driving? Use the distance formula d=rt.
A.27 mph
B.29 mph
C.37 mph
D.17 mph
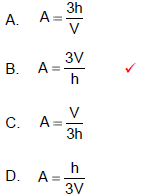
Practice Exercise 3
Solve the formul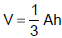a 
for A
Practice Exercise 4
Solve the formula for y: 2x + 3y = 6
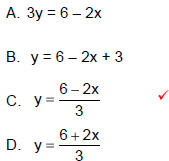
Practice Exercise 5
Solve the formula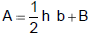 
for
b
Practice Exercise 6
Find the length of a rectangular garden with a perimeter
of 94
meters if the length is 5 meters more than the width.
A.52 meters
B.26 meters
C.21 meters
D.47 meters
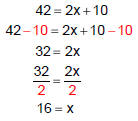
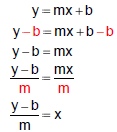
