POLYNOMIALS
The material in this chapter is fairly informal. Unlike earlier chapters, no
attempt is made to rigorously prove the results contained here
1. Polynomial Rings
definition 1. Let R be a commutative ring, and x a variable. Then R[x]
is the set of polynomial
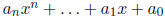with coefficients
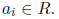
Example. Observe that
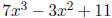is in Z[x]. It is also in Q[x], in R[x],
and in C[x] since
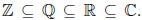Observe that
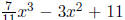is in
Q[x] but not in Z[x]. Observe that
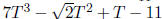is in R[T] but not
in Q[T]. Observe that Z - i is in C[Z] but not in C[S].
If
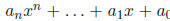is a polynomial with coefficients
,
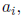we adopt
the convention that ai = 0 for all values of i not occurring in the expression
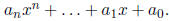For example, when writing
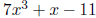in the form
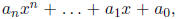we consider
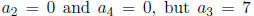and
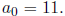Two polynomials
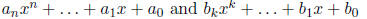
are defined to be equal if and only if
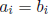for all
Example. Observe
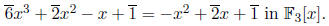
Among the polynomials in R[x] are the constant polynomials a0. In other
words,
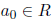can be thought of as both an element of R and as a constant
polynomial in R[x]. Thus
We define multiplication and addition of polynomials in the usual way.
For example, in
the product of
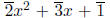with
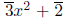can be
computed as follows
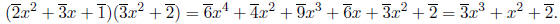
Exercise 1. Multiply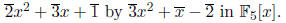
The set R[x] is closed under addition and multiplication. So + and *
give two binary operations
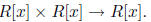
Lemma 1. If R is a commutative ring, then addition and multiplication
are
associative and commutative on R[x]. In addition, the associative law holds.
Lemma 2. If R is a commutative ring, then the constant polynomial 0 is
an
additive identity for R[x], and the constant polynomial 1 is a multiplicative
identity for R[x].
Theorem 3. If R is a commutative ring, then R[x] is also a commutative
ring.
2. Substitutions
definition 2. If
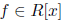then f(a) denotes what we get when we substitute
a for x in f. It is defined whenever the substitution makes sense (typically
when a is in R, or when a is in a ring containing R).
Example. If
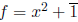in
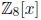then
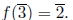
Example. If
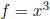in
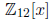then
.
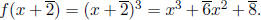(Did
you see what happened to the linear term?).
Example. If
,
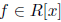and y is another variable, then f(y) is in R[y] and has
the same coefficients. However, if x and y are di erent variables, then f(x)
is not considered to be equal to f(y) unless f is a constant polynomial.
Example. Let
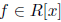Observe that f(x) is just f itself since when we
replace x with x we get what we started with. So f(x) is another way of
writing f. So we can write f as f(x) when we want to emphasize that f is
a polynomial in x.
Example. Here is an amusing example. Let
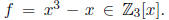Then
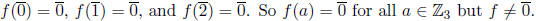So
polynomials cannot be treated as functions when R is nite: two distinct
polynomials, for example f and
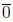as above, can have identical values. This
cannot happen for functions.
definition 3 (Root of a polynomial). Let
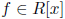and
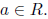If f(a) = 0
then a is called a root of
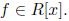
The above example (preceding the definition) shows that every element
of
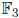is a root of
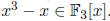
Exercise 2. Find the roots of
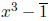in
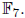Find the roots of
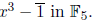
3. The Quotient-Remainder Theorem for Polynomials
Let F be a field. The ring of polynomials F[x] has a quotient-remainder
theorem. To state this theorem we need to discuss a notion of size for F[x]
traditionally called the degree:
definition 4. Let
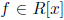where R is a commutative ring. If f has form
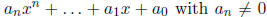then the degree of f is defined to be n
and the leading coefficient is defined to be
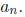
If f = 0 then the degree of f is said to be undefined (some authors give
it degree
).
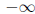Be careful when using this definition in modular arithmetic. For example,
6x3 + 2x2 - x + 1 in F3[x] has only degree 2, and 6x3 + 2x2
- x + 1 in F2[x]
has degree 1. However, 6x3 + 2x2 - x + 1 in F5[x] has degree 3
You would hope that the degree of fg would be the sum of the degrees of
f and g individually. However, examples such as (2x2 + 3x + 1)(3x2 + 2) =
3x3 +x2 +2: in Z6[x] spoil our optimism. However, if the
coefficients are in
a field F then it works.
Theorem 4. If f,
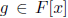are non-zero polynomials where F is a field,
then
deg(fg) = deg f + deg g:
Informal Exercise 3. Justify the above theorem. Explain why the proof does
not work if the coefficients are in Zm where m is composite. Hint: focus on
the leading coefficients.
As mentioned above, the degree of a polynomial is a measure of size.
When we divide we want the size of the remainder to be smaller than the
size of the quotient. This leads to the following:
Theorem 5 (Quotient-Remainder Theorem). Let f,
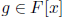be polynomials
where F is a field. Assume g is not zero. Then there are unique polynomials
q(x) and r(x) such that (i) f(x) = q(x)g(x) + r(x), and (ii) the polynomial
r(x) is either the zero polynomial or has degree strictly smaller than g(x).
Remark 1. The polynomial q(x) in the above is called the quotient and the
polynomial r(x) is called the remainder.
Remark 2. This theorem extends to polynomials in R[x] where R is a com-
mutative ring that is not a field, as long as we add the extra assumption
that the leading coefficient of g is a unit in R.
Remark 3. We could use this theorem as a basis to prove theorems about
GCD's and unique factorization in F[x].
As an important special case of the above theorem, consider g(x) = x-a
where a ∈,R. Then the remainder r(x) must be zero, or have
degree zero.
So r = r(x) is a constant polynomial. What is this constant? To find out,
write f(x) = q(x)(x - a) + r. When we substitute x = a we get
f(a) = q(a)(a - a) + r = 0 + r = r:
In other words, r = f(a). This gives the following:
Corollary 6. Let a ∈,F where F is a field, and let f ∈,F[x]. Then there is
a unique polynomial q ∈,F[x] such that
f(x) = (x - a)q(x) + f(a):
Remark 4. This actually works for commutative rings as well as for
fields F
since the leading coefficient of g(x) = x - a is 1 which is always a unit.
The following is a special case of the above corollary (where f(a) = 0).
Corollary 7. Let a ∈,F where F is a field, and let f ∈,F[x]. Then a is a
root of f if and only if (x - a) divides f.
4. The number of roots
Theorem 8. Let f ∈,F[x] be a nonzero polynomial with
coefficients in a
field F. Then f has at most n = deg f roots in F.
Proof. This is proved by induction. Let S be the set of natural numbers n
such that every polynomial f that has degree n has at most n roots in F.
Our goal is to show that S = N.
Showing 0 ∈S is easy. If f is a non-zero constant
polynomial of degree 0,
then it has 0 roots since it is a nonzero constant polynomial.
Suppose that k ∈S. We want to show k + 1
∈,S. To do so, let f be a
polynomial of degree k+1. If f has no roots, then the statement is trivially
true. Suppose that f does have a root a ∈,F. Then, by
Corollary 7,
f(x) = q(x)(x - a):
By Proposition 4, deg f = 1 + deg q. In other words, deg q = k. By the
inductive hypothesis k 2 S, the polynomial q has at most k roots.
We will now show that the only possible root of f that is not a root of
q is a (but a could also be a root of q). Suppose that f has a root b
≠, a.
Then 0 = f(b) = q(b)(b-a). Since b-a ≠, 0, we can multiply both sides by
the inverse: 0(b-a)-1 = q(b)(b-a)(b-a)-1. Thus 0 = q(b). So every root
of f not equal to a must be a root of q(x). Since q(x) has at most k roots,
it follows that f(x) must have at most k + 1 roots. So k + 1 2 S.
By the principle of mathematical induction, N = S. The result follows.
Remark 5. Observe how this can fail if m is not a prime. The polynomial
x2 - 1 2 Z8 has degree 2, yet it has four roots! (Can you find them?)
Informal Exercise 4. Show that if f, g ∈,F[x]
are non-zero polynomials
where F is a field, then the set of roots of fg is the union of the set of roots
of f with the set of roots of g.
Exercise 5. Show that the result of the above exercise does not hold Z8[x]
by looking at
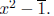
Informal Exercise 6. Although the result of Exercise 4 does not hold if F is
replaced by a general commutative ring (such as Zm where m is composite),
one of the two inclusions does hold. Which one and why?
5. Irreducible Polynomials
One can prove unique factorization into irreducible polynomials for F[x].
A polynomial f ∈,F[x] is said to be
irreducible if it is not a constant and
if it has no divisors g with 0 <, deg g <, deg f. These polynomials play the
role of prime numbers in polynomial rings. One can use the methods of
Chapter 4 to prove that every polynomial is the product of a constant times
irreducible polynomials.
Finally, even if F is nite, one can prove that there are an in nite number
of irreducible polynomials in F[x] using a similar argument to that used in
showing that there are an in nite number of primes.
6. Fundamental Theorems
Theorem 9 (Fundamental Theorem of Algebra, Part 1). Every nonconstant
polynomial in C[X] has a root in C.
Corollary 10. Every non-constant polynomial with real or complex coe -
cients has a root in C.
Corollary 11 (Fundamental Theorem of Algebra, Part 2). Every non-
constant polynomial in C[x] is the product of linear polynomials in C[x].
For real roots we get the following weaker results:
Theorem 12. Every polynomial of odd degree in R[x] has a root in R.
Real polynomials do not always factor into linear real polynomials. The
following weaker result is true:
Theorem 13. Every non-constant polynomial in R[x] factors into a product
of linear and quadratic real polynomials in R[x]
In other words, we have to allow for the possibility of quadratic factors
that have no real roots. The irreducible polynomials of R[x] are the lin-
ear polynomials and the quadratic polynomials with negative discriminate.
Contrast this with C[x] where the irreducible polynomials are just the linear
polynomials.
In Q[x] the situation is even worse. We can find polynomials of any degree
that have no roots in Q, and we can find polynomials of any degree that are
irreducible, and do not factor into smaller degree factors.
Exercise 7. Factor x4-1 into irreducible polynomials in C[x]. Factor x4-1
into irreducible polynomials in R[x].