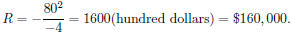Math 165 Linear Price - Demand Model and Parabolas

A typical problem about maximizing revenue

A manufacturer determines that when x hundred units of a particular commodity are
produced, they can all be sold for a unit price given by the demand function p = 80 - x
dollars. What is the maximum revenue (in dollars)?

The demand function is linear - the quantity (demand) x and the price p are related by
a linear relation. The problem is to set the price p (or demand x) so that the revenue R,

R = p · x hundred dollars

is maximized.

Notice that

R = (80 - x)x

is a quadratic function of x; moreover, the coefficient of x² is negative, so the graph of
R(x) is a parabola opening downward. We even have that the parabola is presented in a
factored form with roots at x = 0 and x = 80.

If we graph the parabola, it appears that R is maximized at the vertex of the parabola
which occurs when x = 40, halfway between the roots!

We are already familiar with the quadratic formula for the roots of the equation

Ax² + Bx + C = 0

occur at



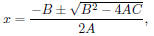
with the usual remarks about the case B² - 4AC ≤ 0.

The quadratic formula is very much related to the process called completing the square -
write



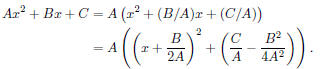
It is apparent that the vertex of the parabola is located at

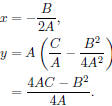
If A > 0, the graph opens upward and the quadratic function has a minimum value at
the vertex.

If A < 0, the graph opens downward and the quadratic function has a maximum value
at the vertex.

In our example A = -1, B = 80, C = 0. The revenue is maximized when

x = -B/2A = 40(hundred units);
p = (80 - 40) dollars;