MATH 134 Revision Notes
Study all homework and exercises
1
.1a. Find the intercepts of and graph the line 5x + 9y
b
. Find the distance,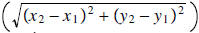
between two given points. Find the midpoint
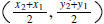of two given points. e.g. find the
distance and midpoint of the points (4.6,-3)
and (6,2.5).
c. Equation of circle in standard form is:
(x-h)2 + (y-k)2=r2 where (h ,k) is the center and
r is the radius. For examples, find the equation
of the circle if (i) r=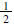
,
center (-1,4); (ii) center =(3,-6)
and passing through the point
(0, 4). Find the center and radius of the circle for (x-3)2
+ (y+5)2 = 9.
1.2
a. Determine a relation expression whether it is
a function, and identify the domain and range.
For examples, {(4,-14),(5,8),(0,19),(6,8)} and
Study the questions 15-20, 35-39, and 55-61.
b. Find the function values. e.g. f (x) = 6x2 - 9x, find f(2),f(10),f(-x),f(1-h) and f (x+h).
c. Find the domain for a give function. e.g.
f (x)
= x2 + 10x + 15,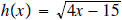
,
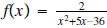
1.3
a. Slope =
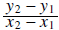, e.g. find the slope of the straight line passing through
(8,-2)and (-1,5); Graph the linear equation and determine its slope (a) 4x
- 7y = 20, (b) y = -5, (c) x = 6.
b. Study word problems Questions 41-44 and 49.
i. The average weight of a baby born in 1900 was 6. 25 pounds. In 2000, the average weight of a newborn was 6. 625 pounds. we will assume for our purposes that the relationship is linear. Find an equation that relates the year to average weight of a newborn. Using that equation, predict the average weight of a newborn in 2035.
1.4
a. Write a
slope-intercept equation for a line with the given conditions e.g. determine the equation of a straight if (i) m
= 
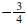and passing through the point (2,-7), (ii) passes through the points (8,4) and
(-2,-6).
b. Write equations of the horizontal and vertical lines which passes through (9,-5).
c. Transform the equation of the straight line from general form to the slope intercept form.
e.g.: Find the slope and y-intercept of 7x + 4y = 10.
d. Determine the equation of the straight line which is parallel or perpendicular the given line
e.g. parallel/ perpendicular to the line 2x - 5y = 10 and containing the point (9,3), and questions 75 to 80 on pp. 116-117.
1.5
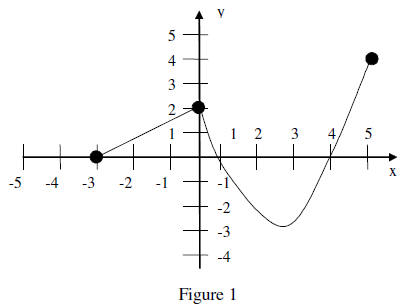
a. In Figure 1 above,
determine the intervals on which the function is (a) increasing, (b) decreasing, (c) constant, (d) relative maximum or minimum.
b. Study the word problems Questions 31-34 on pp. 129-130.
c. Know how to find the function value of a piecewise function.
For example, compute the function value for piecewise function e.g.
,
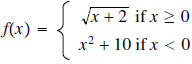find f(-1) and f(6).
1.6
a. Find (f + g)(x),(f - g)(x),(f•g)(x),
and (f/g)(x) ; determine their domains. e.g.
f(x) = 5x - 8 and
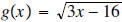
b. Know how to graph and find the domain the function of f + g if the graphs of f(x) and g(x) are given.
c. Find
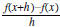if f (x) = 8x2 + 15x
d. Find
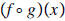and
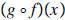and their domain if (a) f
(x)=9x
+ 4 and
,
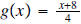(b) f
(x)=
2x + 5 and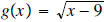
.
e. Find f(x) and g(x)
such that
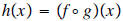when
.
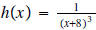1.7
a. Given a graph, should know whether it is
symmetric with respect to the x-axis,
y-axis, and/or the origin; whether the function is even, odd, or
neither.
b. Vertical shift: y f(x)
+ k;
Horizontal shift: y = f(x- h);
Vertical stretch/compression:
y = af(x);
Horizontal stretch/compression y
= f(ax);
Reflection to the x-axis
y
= -f(x) and reflection to the y-axis
y =f(-x).
For examples, write the function and sketch the corresponding graph of
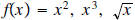, but is (a) shifted left by 3 units; (b)
shifted down by 5 units; (c) vertically sketched by factor of 2 and
shifted up by 3 units; (d) reflection about the
x-axis. Also, suppose that you
are given the graph of f(x) = x2,
graph the functions g(x) = 4(x-1)2 - 2 and
.
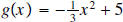2.3 Methods to solve quadratic equations include FACTORING, COMPLETING THE SQUARE, QUADRATIC FORMULA. For examples, solve x2 - 6x - 16; 2x3 - x2 - 6x = 0; 3t2 + 5t - 3 = 0 by using any method mentioned above. Use completing square to solve 2x2 + x - 1 = 0
2.4
a. Find the vertex, axis of symmetry, maximum or
minimum value of the function if y = -(x - 6)2 + 8.
b. Quadratic function is defined as f(x) = ax2 + bx + c. The graph of f(x) is opened upward if a>0 and downward if a<0.
c. Vertex of
f(x) is: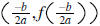
,
axis of symmetry is 
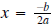. For example, determine
the functions whether they are open up or down, find the vertex, whether there
is maximum or minimum value, range, intervals of increasing and decreasing of
f(x) = -2x2 + 3x + 5 and g(x) = 4x2 - 2x + 1. Sketch the graph of the function.
d. Know how to solve word problems. Study the questions 37-45 on pp. 227 - 228.