Math 132 TEST #2 Solutions
| Problem | 1 | 2 | 3 | 4 | Total |
| Possible Score | 25 | 70 | 40 | 65 | 200 |
| Your Score |
SHOW ALL WORK. Any solution that is not accompanied by the
appropriate work necessary for solving
the problem will receive no credit. If you need more space, you may use the back
of the page.
1. (25 pts) Find a polynomial with the following graph.
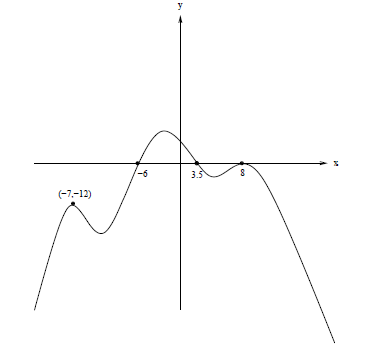
SOLUTION:
The zeros of the polynomial are x = −6, 3.5, and 8, so the
polynomial has the form
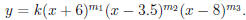
Since the graph bounces off the x-axis at x = 8, we have
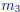 is even, and since the
is even, and since the
graph crosses the x-axis at x = −6 and x = 3.5, we have
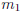 and
and 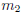 are
odd.
are
odd.
Since there are 5 turning points, 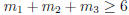 , so let
, so let
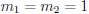 and
and 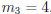 , so
, so
we have y = k(x + 6)(x − 3.5)(x − 8)4.
To solve for k, we let x = −7 and y = −12 to get
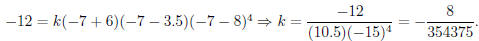
Thus, a polynomial would be
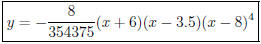
2. Let

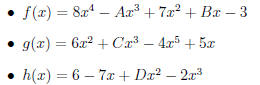
where A, B, C, and D are real numbers.
(a) (7 pts) What do the y-values approach as x→∞ for j(x) = f(x) · g(x)?
SOLUTION: As 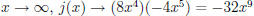 so
so

(b) (7 pts) What do the y-values approach as x→−∞ for k(x) = f(x) · h(x)?
SOLUTION: As 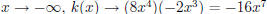 so
so

(c) (7 pts) What do the y-values approach as x→∞ for
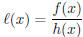 ?
?
SOLUTION: As 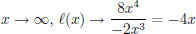 ,so
,so

d) (7 pts) What do the y-values approach as x→−∞ for
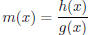 ?
?
SOLUTION: As 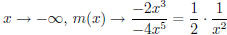 , so
, so

Reminder
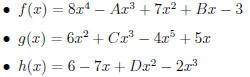
where A, B, C, and D are real numbers.
(e) (15 pts) What are the possible vertical asymptotes of
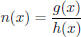 ?
?
SOLUTION:
The possible vertical asymptotes are the zeros of the
denominator, h(x).
Thus, the possible vertical asymptotes have the form
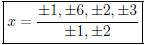
(f) (12 pts) What are the possible zeros of 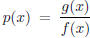 ?
(Hint: you may need to do some
?
(Hint: you may need to do some
factoring).
SOLUTION:
The possible zeros are the zeros of the numerator, g(x) =
6x2 + Cx3 − 4x5 + 5x.
Since there is not a constant coefficient, x = 0 is a zero of g(x).
For other possible zeros, we factor an x from g(x) to get g(x) = x(6x + Cx2
− 4x4 + 5).
Therefore, the possible zeros have the form 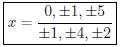
(g) (15 pts) What are the possible holes in the graph of
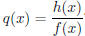 ?
?
SOLUTION:
The possible holes in the graph are the zeros of both the
numerator and denominator.
The possible zeros of h(x) have the form 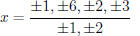
The possible zeros of f(x) have the form 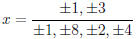
So the possible holes have the form 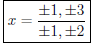
3. Let f(x) = 4x2 + 10x + 9.
(a) (15 pts) Complete the square to write f(x) in the form k(x + h)2
+ v.
SOLUTION:
4x2 + 10x + 9 = k(x + h)2 + v = kx2
+ 2khx + (h2k + v).
Thus, k = 4, and 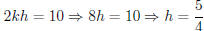 .
.
So 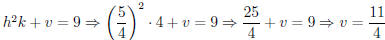
.
Therefore, 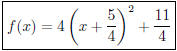
(b) (15 pts) Use part (a) to find the x-values such that f(x) = 4.
SOLUTION:
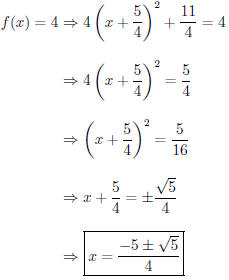
(c) (10 pts) What is the smallest y-value of f?
SOLUTION: Since f is a parabola with vertex 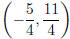 ,
the smallest y-value is
,
the smallest y-value is 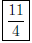
4. Let f(x) = 2x3 + 5x2 − 13x + 5
and g(x) = 2x3 − 15x2 + 18x + 35.
(a) (20 pts) Find the zeros of f(x). Hint: you will probably need to use
the Rational Zeros
Theorem, long division of polynomials, and the quadratic formula (or completing
the square).
You must show all of your work for each of these steps. You may not find the
zeros by graphing
the function with your graphing calculator and having the calculator compute the
zeros for you.
SOLUTION: The possible rational zeros of f(x) are of the form
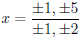 .
.
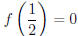 , so 2x − 1 is a factor of f(x). By long
division, we get
, so 2x − 1 is a factor of f(x). By long
division, we get
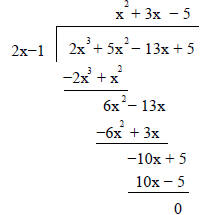
So f(x) = (2x − 1)(x2 + 3x − 5).
Using the quadratic formula, the remaining zeros are
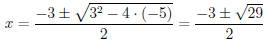 , so the zeros are
, so the zeros are
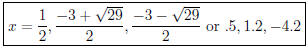
Reminder f(x) = 2x3 + 5x2 − 13x + 5
and g(x) = 2x3 − 15x2
+ 18x + 35.
(b) (20 pts) Find the zeros of g(x). Hint: you will probably need to use
the Rational Zeros
Theorem, long division of polynomials, and the quadratic formula (or completing
the square).
You must show all of your work for each of these steps. You may not find the
zeros by graphing
the function with your graphing calculator and having the calculator compute the
zeros for you.
SOLUTION:
The possible zeros of g(x) have the form
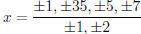 .
.
From these we find g(−1) = 0, g(5) = 0, and 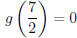 .
.
Thus, the zeros are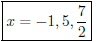 .
.
Reminder f(x) = 2x3 + 5x2 − 13x + 5
and g(x) = 2x3 − 15x2
+ 18x + 35.
(c) (25 pts) Use parts (a) and (b) to sketch the graph of
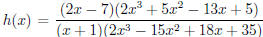
.
Mark any x-intercepts, y-intercept, horizontal asymptote, vertical asymptotes,
and holes. You
must show all of your work on this problem including any work involving
asymptotes.
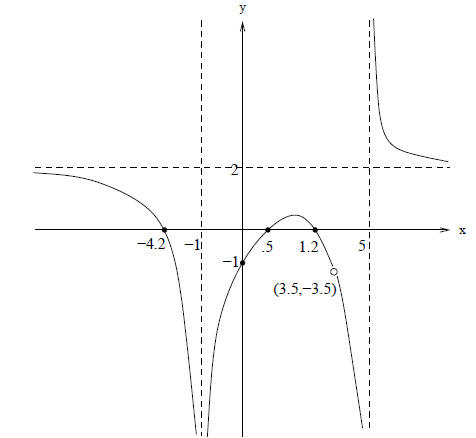
SOLUTION:
From parts (a) and (b), we can factor
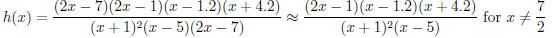
The zeros are x = .5, 1.2,−4.2, and the y-intercept is
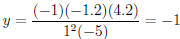 .
.
As 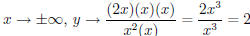 , so y = 2 is a horizontal asymptote.
, so y = 2 is a horizontal asymptote.
As 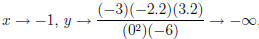 , so x = −1 is a vertical asymptote.
, so x = −1 is a vertical asymptote.
As 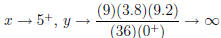 , so x = 5 is a vertical asymptote.
, so x = 5 is a vertical asymptote.


