Matrix Operations with Mathematica
In the symbolic math program Mathematica, a matrix is a
list whose entries are the matrix’s rows. Each
row in turn is a list of numbers. Lists in Mathematica are
collections of things separated by commas and
enclosed in curly brackets.
For example,
{{1,−1, 0}, {2,−4, 6}} represents the matrix 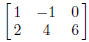 .
.
(In these examples, the input to Mathematica is on the first line, and the
output is indented on the
second line.)
The curly bracket notation for matrices can be hard to read. If you want a
matrix displayed in standard
matrix form, put // MatrixForm at the end of the line:
{{1, -1, 0}, {2, -4, 6}} // MatrixForm
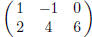
You can add or subtract matrices using + or −. For example,
{{1, -1, 0}, {2, -4, 6}} + {{7, 1, 3}, {0, 3, -6}}
{{8, 0, 3}, {2, -1, 0}}
Multiply a matrix by a number by placing the number in front of the matrix:
3{{1, -1, 0}, {2, -4, 6}}
{{3, -3, 0}, {6, -12, 18}}
IdentityMatrix[n] represents the n ×n identity matrix. (Notice the square
brackets around the “n”.)
IdentityMatrix[2]
{{1, 0}, {0, 1}}
If m is a matrix, its transpose is given by Transpose[]:
Transpose[{{1, -1, 0}, {2, -4, 6}}]
{{1, 2}, {-1, -4}, {0, 6}}
If m is a matrix, its inverse is given by Inverse[m]:
Inverse[{{1, 2}, {3, 4}}]
{{-3, 2}, {2, -1}}
To multiply two matrices, put a period between them:
m = {{1, -3}, {2, 3}, {6, 0}}. {{a, b}, {c, d}}
{{a - 3c, b - 3d}, {2a + 3c, 2b + 3d}, {6a, 6b}}
Notice that Mathematica has no problem with symbolic matrices. Also, notice that
I set the preceding
expression equal to m. This is a good idea if you want to refer to things you’ve
entered earlier.
Here are some Mathematica functions which perform row
operations. You can use them to get a feel for
how to do a row reduction without getting caught up in the tedious arithmetic.
RowSwap[matrix_, row1_, row2_] :=
Block[ {temp = matrix},
temp[[row1]] = matrix[[row2]];
temp[[row2]] = matrix[[row1]];
temp
]
RowMult[matrix_, row_, factor_] :=
Block[ {temp = matrix},
temp[[row]] = factor matrix[[row]];
temp
]
RowComb[matrix_, row1_, row2_, factor_] :=
Block[ {temp = matrix},
temp[[row1]] =
matrix[[row1]] + factor matrix[[row2]];
temp
]
For example, the following command does 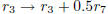 on mymatrix — i.e. row 3
is replaced with
on mymatrix — i.e. row 3
is replaced with
row 3 plus 0.5 times row 7 — and returns the result:
RowComb[mymatrix, 3, 7, 0.5]
This command swaps rows 3 and 7 of mymatrix and returns the result:
RowSwap[mymatrix, 3, 7]
This command multiplies row 4 by 17 and returns the result:
RowMult[mymatrix, 4, 17]
Warning: The functions above simply return the results of performing the
operations — they don’t
change the original matrix. If you want to change the matrix as you go, you
should do something like
this:
mymatrix = RowSwap[mymatrix, 3, 7]
This swaps rows 3 and 7 of mymatrix, and changes mymatrix accordingly. However,
if you mistype
something and produce an error, mymatrix will be messed up — so be careful!
The commands above will work on any matrix. For example, if you’re row reducing
matrices over Z5, use
the commands above to row reduce, then do the following to reduce everything mod
5 at the end (assuming
that the matrix is mymatrix):
Mod[mymatrix, 5]
Mathematica has a built-in function which does row reduction in one shot. This
command gives the
row-reduced echelon form for mymatrix:
RowReduce[mymatrix]
Note that it only works on matrices with real or rational entries; you can’t use
it as is to row reduce
matrices over Zn.


