Quadratic Functions and Graphs
4-4 Solving Equations Using Factoring - Two Days
Warm-up
1. Find the area of a square whose sides are 12 m long.
2. Find the product of 2x(x + 1).
3. Find the product (2x + 1) (x + 1).
4. If 2ab = 0 and a = -1, what is the value of b?
5. What is the greatest common factor of 6, 15, and 21?
Answers to warm-up
1. Area is 144 m2
2. 2x2 + 2x
3. 2x2 + 3x + 1
4. b = 0
5. GCF is 3
4-4 Solving quadratic equations by factoring
A trinomial is an expression that can be written as the sum of 3 unlike terms
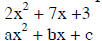
Factoring is undoing FOILing. The trinomial will factor
into two binomials.
Examples 1-4 show how to factor when a = 1. Example 5 shows how to factor when a
≠1.
Factoring when a = 1
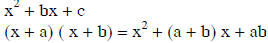
• If c is positive, then the factors are either both
positive or both negative.
o If b is positive, then the factors are positive
o If b is negative, then the factors are negative.
o In either case, you're looking for factors that add to b.
• If c is negative, then the factors you're looking for are of alternating
signs; that is, one
is negative and one is positive.
o If b is positive, then the larger factor is positive.
o If b is negative, then the larger factor is negative.
In either case, you're looking for factors that are b units apart.
Example 1
Factor x2 - 9x + 18 (ax2 + bx + c)
| Solution | |
| (x ____)(x ____) | |
| List the factors of 18 | (the c) |
| -9 ·- 2 | Factors must add up to –9. So, one factor + and one factor is - |
| 2 · 9 | |
| -6 · -3 | |
| 3 · 6 | |
| -18 · -1 | |
| 1 · 18 |
Guess and check
( x-9)( x-2) =x2-11x+18 ←no
( x+9)( x-2) =x2+11x+18 ←no
(x- 3)( x-6) =x2-3x-6x+18←yes
Example 2
Factor x2 +3x + 2
| Solution | |
| (x ____)(x ____) | |
| Factors of 2 | Add up to 3 |
| 2·1 | Yes |
| 1·2 | Yes |
Guess and check
(x + 2)(x +1) = x2 + 2x + x +1= x2 +
3x +1
←
yes!
Example 3
Factor x2 -3x - 40
| Solution | |
| (x ____)(x ____) | |
| Factors of –40 | Add up to -3 |
| -8 · 5 | Yes |
| -5 · -8 | No |
| -2· 20 | No |
| -20 · 2 | No |
(x-8)(x+5)
Check
(x-8)(x+5)=x2 -8x +5x-40= x2 -3x - 40
Example 4
Factor x2-x - 6
| Solution | |
| (x ____)(x ____) | |
| Factors of –6 | Add up to -1 |
| -2 · 3 | No |
| -3 · 2 | Yes |
(x-3)(x+2)
Check
(x-3)(x+2)=x2-3x +2x- 6= x2-x - 6
Sometimes a (the x2coefficient) is not 1.
Example 5
Factor 2x2 − 7x −30
Solution
x2 − 7x −30
Use guess and check!
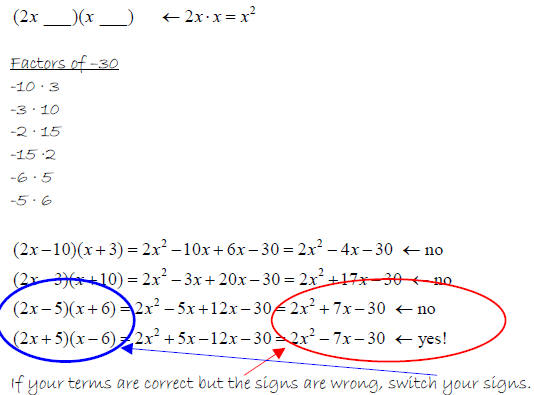
4-4 Solving equations by factoring – Day 2
Factoring when a ≠1
Example 1
Factor 3x2 +11x +10
Solution
| Factors of | Factors of c | Product |
| 3 • 1 | 10 • 1 | (3x + 10)(x + 1) |
| 1 • 3 | 10 • 1 | (x + 10)(3x + 1) |
| 3 • 1 | 5 • 2 | (3x + 5)(x + 2) → 3x2 + 11x + 10 ←This is correct! |
| 1 • 3 | 5 • 2 | (x + 5)(3x + 2) |
(3x + 5)(x + 2)
Example 2
Factor 4x2 −10x −14
Solution
Factor out the greatest common factor.
2(2x2 – 5x – 7)
| Factors of | Factors of c | Product |
| 2 • 1 | -7 • 1 | 2(2x – 7)(x + 1) → 4x2– 10x – 14 ←This is correct! |
| 1 • 2 | -7 • 1 | 2(x – 14)(4x – 1) |
| 2 • 1 | 7 • -1 | 2(2x – 14)(2x + 1) |
| 1 • 2 | 7 • -1 |
(4x – 14)(x + 1)
Special Factoring Patterns – Yellow box on page 208
| To factor a difference of two squares: | Examples |
| a2 −b2 = (a + b)(a − b) | 9x2−100 = (3x +10)(3x −10) |
| To factor a perfect square trinomial: | |
| a2 + 2ab + b2 = (a + b)2 | 16x2 + 20x +169 = (4x +13)2 |
| a2 − 2ab + b2 = (a − b)2 | 4x2 − 20x + 25 = (2x − 5)2 |
Guidelines for factoring completely – Yellow box on page 210
1. Factor out the greatest common factor first.
2. Look for a difference of two squares.
3. Look for a perfect square trinomial.
4. If a trinomial is not a perfect square, use trial and error to look for a
pair of factors.
Example 3
Factor 25x2 - 81
Solution
Test whether the expression is a difference of two squares. Ask these questions:
• Is the expression a difference? Yes
• Is the first term a square? Yes
• Is the second term a square? Yes
To factor a difference of two squares:
a2 −b2 = (a + b)(a − b)
(5x + 9)(5x – 9)
Example 4
Factor 16x2 + 56x + 49
Solution
Test whether the trinomial is a perfect square trinomial. Ask these questions:
• Is the first term a square? Yes
• Is the last term a square? Yes
• Is the middle term twice the product of
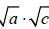? Yes, 4 • 7 = 28, which is ½ of 56.
To factor a perfect square trinomial:
a2 + 2ab + b2 = (a + b)2
a2 − 2ab + b2 = (a − b)2
(4x + 7)2
Solving equations by factoring
Some quadratic equations can be solved by factoring.
• First the equation must be written in standard form, a x2 + bx + c
• Then, if the trinomial is factorable, the equation can be solved using
the zero-product
property.
Zero-product property (ZPP)
If ab = 0, then a = 0 or b = 0 or both are zero.
Example: If y (x + 5) = 0, then y = 0 or x + 5 = 0, or both.
Example 6
Solve 6x = x2 + 9
Solution
x2 - 6x + 9 = 0 ← Rewrite equation in standard form.
The equation is a perfect square trinomial.
To factor a perfect square trinomial:
a2 + 2ab + b2 = (a + b)2
a2 − 2ab + b2 = (a − b)2
So, the equation factors into
(x + 3)(x + 3) = 0
Set each factor equal to zero (ZPP) and solve for x.
x + 3 = 0 or x + 3 = 0
x = -3 or x = -3
Example 7
Solve 8x2 - 18x = -4
Solution
8x2 - 18x + 4 = 0 ←Rewrite equation in
standard form.
2(4x2 - 9x + 2) = 0 ←Factor out the
greatest common factor, 2.
4x2 - 9x + 2 = 0 ←Divide both sides by 2
(4x – 1)(x – 2) = 0 ←Factor the trinomial
4x – 1 = 0 or x – 2 = 0 ←Set each factor equal to 0
and solve for x. (ZPP)
x = ¼ or x = 2
There where three factors that multiplied to 0. Why didn’t we set all three of
them equal to
zero when solving?