Factoring and Quadratic Equations
Here we will be factoring special binomials. We have seen
some of the formulas in a
previous section but we will be using them in a different manner here. These
formulas
will be used as a template for factoring.
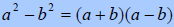 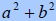 does not factor does not factor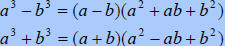 |
Difference of Squares does not factor - Sum of Squares - Difference of Cubes - Sum of Cubes |
The idea is to identify the a and the b then plug in to the formulas above
 |
||
| Step 1: Identify the special binomial. |
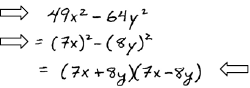 |
No need to check but it doesn’t hurt. |
| Step 1: Identify the special binomial. |
||
| Step 3: Plug into the formula. | 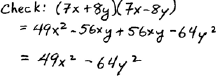 |
The same steps can be used for the sum and difference of cubes formula.
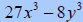 |
|
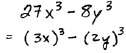 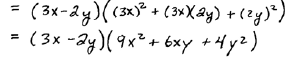 |
Difference of cubes |
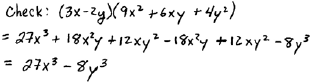 |
At this point it is nice to review the perfect cubes that
we will be likely to run into when
working problems in this section. 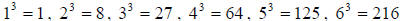
and 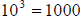 . Many times the coefficients will give a
clue as to what special binomial
. Many times the coefficients will give a
clue as to what special binomial
formula is to be used.
A. Factor
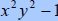 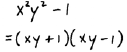 |
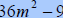 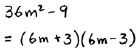 |
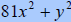 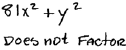 |
|
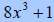 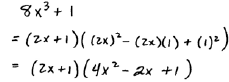 |
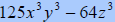 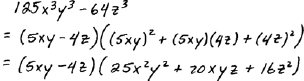 |
||
At this point we will look a bit more closely at the
process in which we are factoring sum
of cubes using the formula 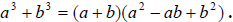
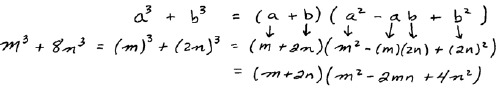
Once we identify the a and the b in the formula it really
is just a matter of plugging in to
the formula or using it as a template. Most of this is done mentally, so it is
sufficient to
present your solution without the above steps.
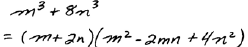
Rest assured that with much practice you will be able to
jump straight to the answer too.
The first step to this ability, of course, is to memorize the formulas.
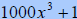 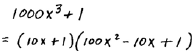 |
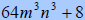 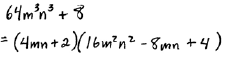 |
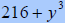 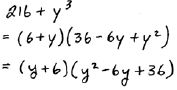 |
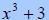 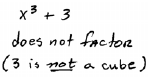 |
As we have seen before, we will often run into polynomials
with a GCF. It is important
with special binomials to factor out the GCF first.
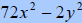 |
||
| Doesn’t really look like difference of squares. | 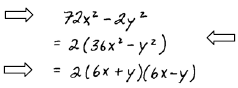 |
Factor out the GCF and it is easier to see. |
| Difference of squares |
B. Factor
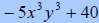 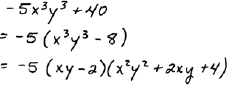 |
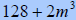 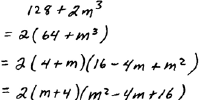 |
|
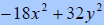 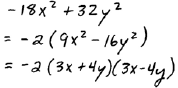 |
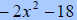 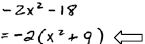 |
|
| Sum of squares does not factor for us. | ||
Factoring binomials is a bit more complicated when larger
exponents are involved. It is
difficult to recognize that x6, for example, is a perfect cube. We can think of
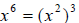
or the cube of x squared. Also, recall the rule of exponents
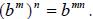
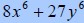 |
||
Sum of cubes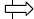 |
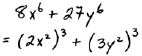 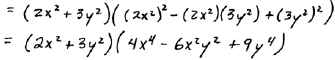 |
Here 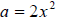 and and
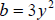 in the formula 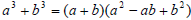  |
It is not always necessary to show all the steps shown
above. Ask your instructor what he
or she wants to see in the way of steps when presenting your solutions in this
case.
C. Factor
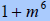 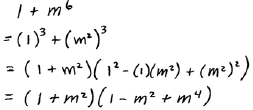 |
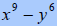 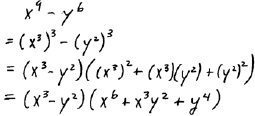 |
||
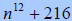 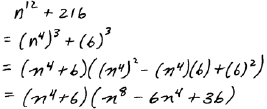 |
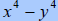 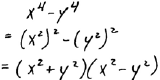 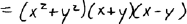 |
||
 |
Factor using difference of squares again. | ||
Tip: Look out for problems that require us to
factor the factors. In other words, look to
continue factoring until all factors are completely factored. Also, the
trinomials that we
get when using the sum and difference of squares will not factor for us so do
not even try.
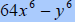 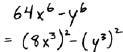 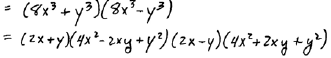 |
 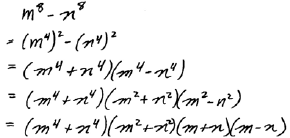 |
|
| ALWAYS factor difference of squares first |
||
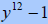 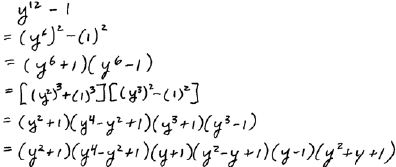 |
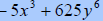 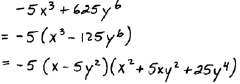 |
|
If we are confronted with a polynomial that is both a
difference of squares and a
difference of cubes we must factor it as a difference of squares first. Doing
this will
ensure that our formulas will achieve the best possible factorization.


