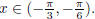Inverse Trigonometric Functions Workshop
1. The inverse of a function f (x), if it exists, is
denoted f -1(x). The range of f -1(x) is equal to the
domain of f (x). However, the domain of sin x is “all real numbers,” but the
range of sin-1 x is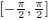 
.
Why is this?
It might help to answer the following question first: Why is
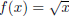not the inverse of g (x) = x2?
Also, 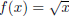has an inverse: what would f -1(x) be?
2. Let c be some constant. The numbers sin-1(c), cos-1(c), and tan-1(c) are best
described as
(a) areas.
(b) angles.
(c) x-coordinates.
(d) y-coordinates.
3. Let c be some constant. The number sin(c) is best
described as
(a) an area.
(b) an angle.
(c) an x-coordinate.
(d) a y-coordinate.
4. Let c be some constant. The number cos(c) is best described as
(a) an area.
(b) an angle.
(c) an x-coordinate.
(d) a y-coordinate.
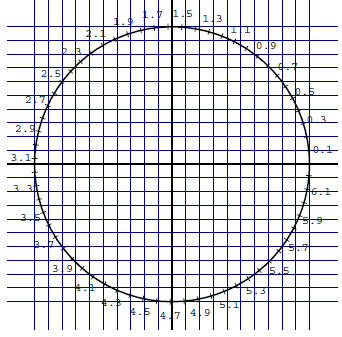
5. Use the calibrated unit circle below to approximate the following. If the answer does not exist, say so.
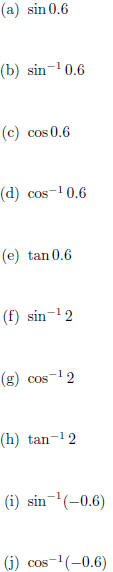
Evaluate the following:
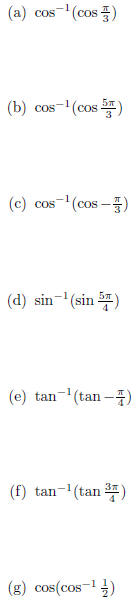
(h)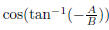 
, where A and B are positive numbers.
(i)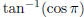
(j)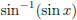 
, where
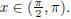
(k)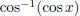 
, where
