College Algebra Study Guide
E.8
27. Show that each function is the inverse of the other: f(x) = 4x - 7 and
.
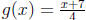Answer: Yes, the functions are inverse of each other. f(g(x)) = x and g(f(x)) =
x.
28. Find the inverse of the function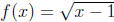 
.
Answer: f -1(x) = x2 + 1 for x ≥ 0
29. Does the graph below represent a function that has inverse function?
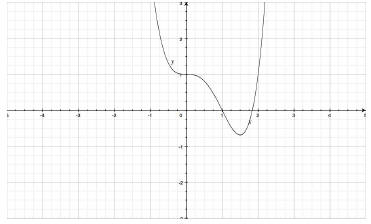
Answer: No, notice that horizontal lines can be drawn and
intersect the graph more than once.
30. The formula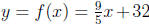 
is used to convert from x degrees Celsius to y degrees Fahrenheit.
Find the formula to convert from y degrees Fahrenheit to x degrees Celsius. Show
that this formula
is the inverse function of f(x).
Answer: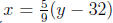 
is the inverse, then
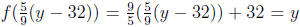, therefore the
formula 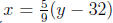is the inverse of f(x).
E.9
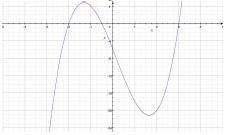
31. Graph the polynomial function: f(x) = 2x3-x2-13x-6. Indicate the graph's end
behavior, the
x-intercepts, state whether the graph crosses the x-axis or touches the x-axis,
indicate the y-intercepts.
If necessary, find a few additional points and graph the function.
Answer: The graph falls to the left and rises to the right, x = -2,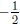
, 3, y = -6. Crosses the
x-axis at every zero since each zero has multiplicity 1.
32. Graph the rational function
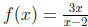. Indicate all x-intercepts, y-intercepts, horizontal asymp-
tote, vertical asymptote(s). If necessary, find a few additional points and graph
the function.
Answer: x = 0, y = 0, vertical asymptote at x = 2, horizontal asymptote at y =
3.
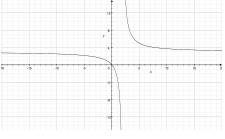
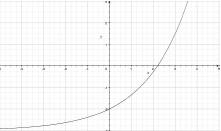
33. Sketch the graph of the exponential function
:
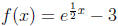Answer: Horizontal asymptote located at y = -3
34. Graph the following Piecewise function and state the
domain, range and intervals where the func-
tion is increasing, decreasing and constant.
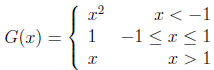
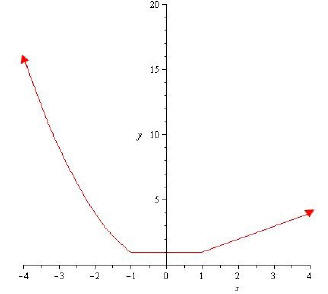
Answer: The domain of this function is the set of all Real
Numbers, the range is the interval
[1,∞). The interval of increasing is (1,∞), the interval of decreasing is (-∞,-1) and the interval
where the function is constant is (-1, 1). See the graph below.
E.10
35. Apply properties of Logarithms to simplify each expression.
Answer: a) 25,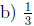 
36. Expand each expression by writing in terms of sum or difference of
logarithms.
Answer: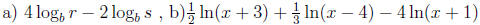 
37. Write the expression as a single Logarithm.
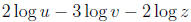
Answer: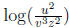
38. Write the expression as a single Logarithm.
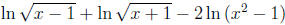
Answer: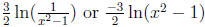
E.11
39. Suppose that y is such that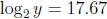 
. Evaluate
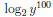
Answer: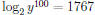 
40. Solve for all the values of x that satisfy the equation:
.
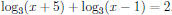Answer: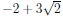 
41. Solve the equation by making an appropriate substitution,
.
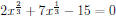Answer: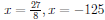
42. Solve the radical equation. Check the proposed solutions.
.
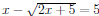Answer: x = 10
43. Find the rational zeros of f. List any irrational zero correct to two
decimal places.
f(x) = x4 + 5x3 - 3x2 - 35x - 28.
Answer: Rational zeros: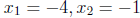 
, Irrational zeros:
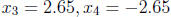
44. Solve the exponential equation. Round your answer to four decimal places.
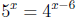
Answer: x = -37.2754
45. Solve the radical equation. Check the proposed solutions.
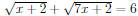
Answer: x = 2, note that x = 14 does not satisfy the original equation.
46. Solve the exponential equation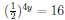 
.
Answer: y = -1.