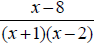Math 161 Final Exam Practice
1. The equation of the x-axis is __________ and the
equation of the y-axis is __________
2. The equation of the unit circle is ______________
3. For the polynomial -2x4 + 5x2 − 2x -5 the degree is _____, the leading
coefficient is _____ and the constant is _____
4. A polynomial with degree 5 has at most ______ zeros.
5. If
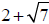is a root of a polynomial with integer coefficients, then so is __________
6. The expression | x − 5 | ≥ 7 means the distance between ____ and ____ is
greater than or equal to_____. Therefore the solution will contain _____
interval(s).
7. An even function is symmetric with respect to __________, whereas an odd
function is symmetric with respect to _______________.
8. An example of an even function is ___________________, and an example of an
odd function is ____________________.
9. A function is one to one if ________________________________________________
10. Any line defines a function except a ____________________ line.
11. The slope of a horizontal line is ______________, whereas the slope of a
vertical line is _______________.
12. The graph of y = x2 looks like
13. The graph of y = (x - 1)2 + 2 looks like
Problems 14 through 23 are worth 4 points each.
14. Find the distance between the points (2,5) and (-4,3), and find the
midpoint.
Distance ____________ Midpoint ( , )
15. Simplify the compound fraction:
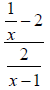
16. Factor the difference of two cubes: x3 − 8y3
17. Rationalize the denominator:
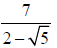
18. Simplify, using positive exponents only:
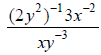
19. Write the equation for the circle with center (0,0) and radius 2.
20. Find the domain of the function
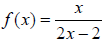
21. Solve the equation (x + 5)2 = 9
22. Solve the equation x2 −2x − 6=0
23. Solve the inequality |x − 5| ≥ 2. Write your answer in interval notation.
Problems 24 through 34 are worth 5 points each.
24. Find the inverse of the function f(x) = 2x − 3.
25. Find the equation of the line through the points (1,3) and (6,-2). Write
your answer in the slope intercept form, i.e. in the form y = mx + b
26. Write the equation for the line with slope 2 through the point (1,5)
For 27 and 28, let
27. Find
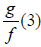
28. Find f ◦ g and g ◦ f
29. Find the vertex and intercepts for the graph of y = x2 - 2x - 3
30. Use synthetic division to show that –1 is a root of f(x)= 2x3 + 3x2 - 5x -
6, and factor f(x) into a linear factor times a quadratic.
31. Find the other two roots for the function in problem 30.
32. Write the function in factored completely as a product of three linear
factors.
33. Find the horizontal and vertical asymptotes if any for the functions
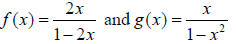
34. Write the partial fraction decomposition for the rational expression
