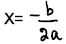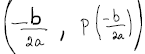Quadratic Functions
| Objectives –
Recognize characteristics of parabolas |
||
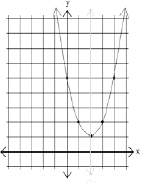
| Quadratic functions, f(x)=ax2 +bx + c graph to be a parabola. |
Parabola • Parabolas
are
|
|
| Special Factored Form of the Quadratic Equation • The vertex of the parabola is at (h,k) and “a” describes the “steepness” and direction of the parabola given by the form f (x) = a(x − h)2 + k |
Minimum or maximum values of a function occur at the VERTEX.
a > 0
parabola opens up (h,k) = minimum point |
|
| Minimum (or maximum) function value for a quadratic occurs at the vertex. • If parabola opens up, f(x) has a minimum value. • If it opens down, f(x) has a maximum value. • Minimum/Maximum values are based on y-values. |
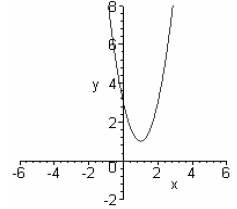
Graph of f (x) = 2x2 − 4x + 3 = 2(x −1)2
|
|
| Vertex Formula P(x) = ax2 + bx + c (a ≠ 0) The following formula will give you the x-value for the vertex of a quadratic:
Coordinates of vertex: |
Example • Determine the following for f(x) without graphing. • f(x) = -3(x – 2)² + 12 a.) Find the vertex. b.) Find the equation of the axis of symmetry. c.) Does f(x) open up or down? d.) Does f(x) have a max. or min. value? Where does this value occur? e.) What is the domain of f(x)? f.) What is the range of f(x)? |
|
| Example • Determine the following for f(x) without graphing. • f(x) = 2x² - 8 x - 3 a.) Find the vertex. b.) Find the equation of the axis of symmetry. c.) Does f(x) open up or down? d.) Does f(x) have a max. or min. value? Where does this value occur? e.) What is the domain of f(x)? f.) What is the range of f(x)? |
To Graph a Quadratic Function 1. Find the coordinates of the vertex. (Use the vertex formula.) 2. Determine which way parabola opens by looking at a. a > 0 parabola opens up (Vertex is lowest point) a < 0 parabola opens down (Vertex is highest point) 3. Find the x-intercept(s). (Set y = 0) 4. Find the y-intercept. (Set x = 0) 2. Graph additional points if needed by t-chart or symmetry. |
|
| Use the vertex and intercepts to graph f(x) = 5 – 4x – x² Give the equation of the axis of symmetry. Determine the domain and the range of f(x).
|