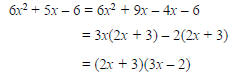Factoring Trinomials36
5.4 Factoring Trinomials
Factoring Trinomials of the Type x2 + bx + c
Factoring Trinomials of the Type ax2 + bx + c,a ≠1
Factoring Trinomials of the
Type x2 + bx + c
When trying to factor trinomials of the
type x2 + bx + c, we can use a trial-anderror
procedure.
Constant Term Positive
Recall the FOIL method of multiplying
two binomials:
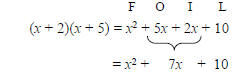
To factor x2 + 7x + 10, we think of FOIL:
The first term, x2, is the product of the
First terms of two binomial factors, so the
first term in each binomial must be x. The
challenge is to find two numbers p and q
such that
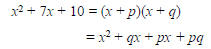
Thus the numbers p and q must be selected
so that their product is 10 and their sum is 7.
In this case, we know from a previous
slide that these numbers are 2 and 5. The
factorization is
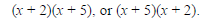
Example Write an equivalent expression
by factoring: x2 + 10x + 21.
Solution
We search for factors of 21 whose sum is 10.

The factorization is thus (x + 7)(x + 3).
Example Write an equivalent expression
by factoring: x 2 – 12x + 20.
Solution
We search for factors of 20 whose sum is –12.

The factorization is thus (x – 2)(x – 10).
Constant Term Negative
When the constant term of a trinomial is
negative, we look for one negative factor
and one positive factor. The sum of the
factors must still be the coefficient of the
middle term.
Example Write an equivalent expression
by factoring: x 2 – x – 20.
Solution
We search for factors of –20 whose sum is –1.

The factorization is thus (x – 5)(x + 4).
Some polynomials are not factorable using
integers.
Example Factor: x2 + 2x + 4
Solution
There are no factors of 4 whose sum is 2.
This trinomial is not factorable into
binomials with integer coefficients.
Tips for Factoring x2 + bx + c
1. If necessary, rewrite the trinomial in descending
order.
2. Find a pair of factors that have c as their product
and b as their sum. Remember the following:
. If c is positive, its factors will have the same
sign as b.
. If c is negative, one factor will be positive and
the other will be negative. Select the factors
such that the factor with the larger absolute
value is the factor with the same sign as b.
Tips for Factoring x2 + bx + c
. If the sum of the two factors is the opposite
of b, changing the signs of both factors will
give the desired factors whose sum is b.
3. Check the result by multiplying the binomials.
Example Factor: x2 - 3xy -28y2
Solution
We look for numbers p and q such that
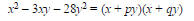
Approach it as though it is x2 – 3x – 28. We look
for factors that multiply to make –28 and whose
sum is –3. Those factors are –7 and 4. Thus,
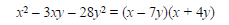
The check is left to the student.
Factoring Trinomials of the
Type ax2 + bx + c (a not 1)
Now we look at trinomials in which
the leading coefficient is not 1.
We consider two methods.
Method 1: Reversing FOIL
We first consider the FOIL method for
factoring trinomials of the type ax2 + bx +c,
where a ≠1.
Consider the following multiplication.
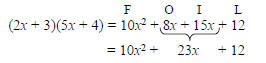
To reverse what we did we look for two binomials
whose product is this trinomial. The product of the
First terms must be 10x2. The product of the Outer
terms plus the product of the Inner terms must be 23x.
The product of the Last terms must be 12.
In general, finding such an answer involves trial
and error. We use the following method.
To Factor ax2 + bx = c by Reversing FOIL
1. Factor out the largest common factor, if one
exists. Here we assume that none does.
2. Find two First terms whose product is ax2:
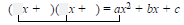
3. Find two Last terms whose product is c:
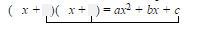
4. Repeat steps (2) and (3) until a combination is
found for which the sum of the Outer and Inner
products is bx:
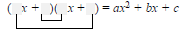
Example Factor: 2x2 + 7x + 6
Solution
1. Observe that there are no common factors
(other than 1 or -1).
2. To factor the first term it must be 2x times x.
(2x + )(x + )
3. The constant term 6, can be factored as
(6)(1), (3)(2), (-6)(-1), and (-3)(-2).
4. Find a pair for which the sum of the Outer
and Inner products is 7x.
Each possibility should be checked by multiplying.
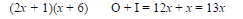
This is not correct. Try again.
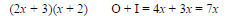
This is the desired factorization.
Tips for Factoring with FOIL
1. If the largest common factor has been factored
out of the original trinomial, then no binomial
factor can have a common factor (except 1, -1).
2. If a and c are both positive, then the signs of the
factors will be the same as the sign of b.
3. When a possible factoring produces the opposite
of the desired middle term, reverse the signs of the
constants in the factors.
4. Keep track of those possibilities that you have
tried and those you that you have not.
Method 2: The Grouping Method
nomials ofthe type ax2 + bx + c, a ≠1, is known as the
grouping method. It involves not only trial
and error and FOIL but also factoring by
grouping.
Example Factor: 4x2 + 16x + 15.
First, multiply the leading coefficient, 4, and the
constant, 15, to get 60. Then find a factorization
of 60 in which the sum of the factors is the
coefficient of the middle term: 16 (in our case 6
and 10). The middle term is then split into the
sum or difference using these factors. Then factor
by grouping.
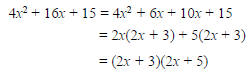
To Factor ax2 +bx + c Using Grouping
1. Make sure that any common factors have
been factored out.
2. Multiply the leading coefficient a and the
constant c.
3. Find a pair of factors, p and q, so that
pq = ac and p + q = b.
4. Rewrite the trinomial’s middle term, bx, as
px + qx.
5. Factor by grouping.
Example Factor: 6x2 + 5x – 6.
Solution
We look for factors of –36 that add to 5. The
factors 9 and –4 are the factors we seek.