A Catalog of Essential Functions
1. Biologists have noticed that the chirping rate of crickets of a certain
species is related to temperature, and the relationship appears to be very
nearly linear. A cricket produces 113 chrips per minute at 70o F and 173 chirps
per minute at 80o F.
(a) Find a linear equation that models the temperature T as a function of the
number of chirps per minutes N.
(b) What is the slope of the graph? What does it represent?
(c) If the crickets are chirping at 105 chirps per minute, estimate the
temperature.
Solution. (a) Graphing T as a function of N, we have the points (113; 70) and
(173; 80) The slope of the line connecting these is
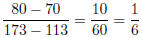
Using the point-slope form, an equation for the line is
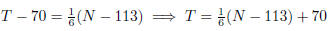
(b) The slope is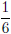
,
meaning that for every six chirps the temperature is one degree higher.
(c) Evalauting at N = 105, we get
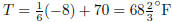
2. The graph of y = f(x) is given. Match each equation with its graph and give reasons for your choices.
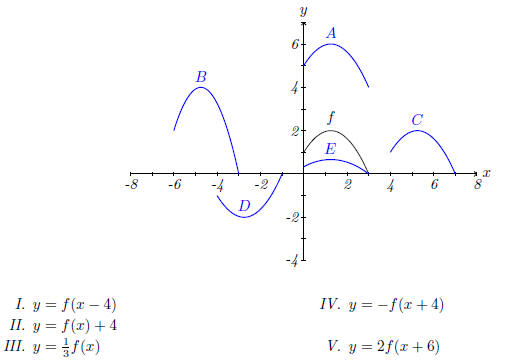
Solution. I. This is the graph of f moved right by 4. Hence the answer is C.
II. This is the graph of f moved up by 4. Hence the answer is A.
III. This is the graph of f scaled vertically by
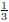. Hence the answer is E.
IV. This is the graph of f, moved to the left by 4, then ipped vertically. Hence the answer is D.
V. This is the graph of f, moved to the left by 6, then scaled by a factor of 2. Hence the answer is E.
3. Graph the function by hand, not by plotting points, but by starting with the graph of one of the standard functions and then applying the appropriate transformations:
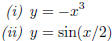
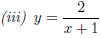
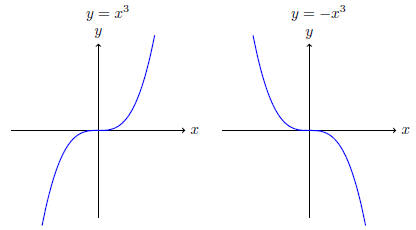
Solution. (i) We take the graph of y = x3 and ip it vertically.
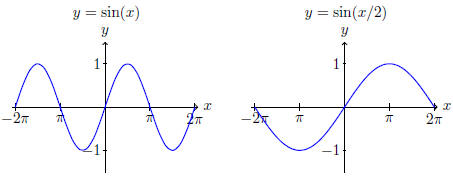
(ii) We take the graph of y = sin(x) and stretch it horizontally by a factor of 2.
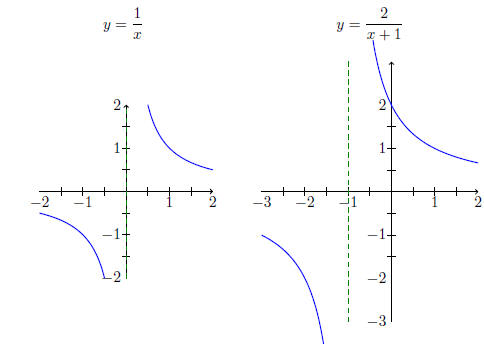
(iii) We take the graph of y =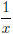
,
move to the left by 1, then scale by 2.
4. Let f(x) = x3 +2x2, g(x) = 3x2 -1. Find f +g, f -g, fg, and f/g and state their domains.
Solution. • f + g = x3 + 5x2 + 1
• f - g = x3 - x2 - 1
• fg = 3x5 + 6x4 + x3 + 2x2. This and the three previous have domain R because they are polynomials.
•
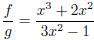. The denominator cannot be zero, so the domain of f=g is
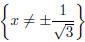
5. Let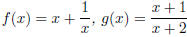
. Find each function and its domain.
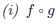
Solution. We have
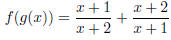
The domain is {x ≠ -1,-2}.
Solution. We have
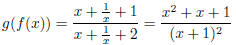
The domain is {x ≠ 0,-1}.
Solution. We have
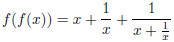
The domain is {x ≠ 0}.
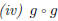
Solution.
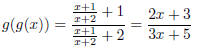
The domain is
.
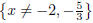6. Express 
as a composition of three functions.
Solution. Let
.
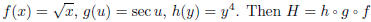