Fractions

Decimal Fractions (pg.13)

▪ Rule: All whole numbers are to the left of the
decimal; all decimal fractions are to the right
of the decimal point.
▪ To read a decimal fraction, read the number
to the right of the decimal and use the name
that applies to the “place value” of the last
figure.
▪ Decimal fractions read with a ths on the end.
▪ To read a whole number and a fraction, the
decimal point reads as an and.

▪ 0.3 = three tenths
▪ 0.5 = five tenths
▪ 1.3 = one and three tenths
▪ 1.5 = one and five tenths
▪ 0.12 = twelve hundreths

Add, Subtract, Divide Decimals

▪ 1.24 + 2.14 = 3.38

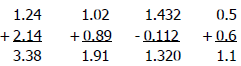
▪ 1.50 ÷ 2 = 0.75
▪ 2.650 ÷ 4 = 0.6625

Round Decimals to nearest
10,100, Whole Numbers

▪ Calculate one decimal place beyond the
desired place.
▪ If the final digit is 4 or less, make no
adjustment.
▪ If the final digit is 5 or more increase the
prior digit by one.
▪ Drop the final digit.

▪ Examples:
• 0.75 = 0.8 0.67 = 0.7 0.125 = 0.13 0.4 =
0.4
• 0.64 = 0.6 0.164 = 0.16 0.6 = 1

Medication Alert!

▪ Do not round medication dosages to
the nearest whole number. This could
result in a medication overdosage.
▪ Rule: Always round your answers to
the nearest measurable dose after you
verify that the dose is correct for that
patient.

Ratio and Proportion

▪ Ratio: Composed of two numbers which
are somehow related to each other. In
dosage problems, ratio is used to
represent the weight of a drug in a
certain volume of solution or package.

▪ Example:
• 1 ml: 100mg (ml contains 100mg of the drug)
• 1 tablet : 50 mg (1 tablet contains 50 mg of the
drug)

Ratio & Proportion

▪ Proportion: Consists of two ratios separated by an
equal sign which indicates that the two ratios are
equal.

▪ Example:
• 1 : 50 = 2 : 100
• 1 ml : 50 mg = 2 ml : 100 mg
• If 1 ml contains 50 mg then 2 ml contains 100mg
• The numbers on the end are called extremes
• The numbers in the middle are called means

▪ Example:
• 1 : 50 = 2 : 100, 1 : 50 = 2 : 100
• 1 times 100 = 100
• 50 times 2 = 100

▪ Ratio and proportion is used in dosage
calculations when only one ratio is known or
complete, and the other ratio is incomplete.

▪ Example: The doctor orders Lasix® 40 mg po stat.
What you have available is Lasix® 20 mg per tablet.

▪ Set up the problem:
• What you have Lasix 20 mg per 1 tablet
• What you want Lasix 40 mg per x tablet
• 20 mg : 1 tab = 40 mg : x tab
20 x = 1 ( 40 )
20 x = 40
x = 40/20
x = 2 tabs

Ratio & Proportion Pointers

* Set your problem up the same way each time. * Write what you have (or the known ratio) first this comes from the drug label. * Write what you want second (or the dosage ordered). * Make the x that you are solving for last. * You must write the ratio in the same

sequence of measurement units or the
answer will be wrong.

Example: mg : ml = mg : ml

▪ Example: The doctor ordered 0.4 mg of
Atropine. The drugs label reads
1000mcg in 2 ml.
• What you have 1000mcg per 2 ml
• What you want 0.4 mg per ml
• To calculate the correct answer you must
first convert all measurement units to be
the same.

STEP 1
Convert 0.4 mg to 400 mcg

1 mg : 1000 mcg = 0.4 mg : x mcg
1x = 1000(0.4)
1x = 400
x = 400/1
x = 400mcg
 

STEP 2
Solving the Problem

What you have 1000 mcg per 2 ml
What you want 400 mcg per x ml (this is the
0.4 mg we converted to mcg in step#1)
1000 mcg : 2 ml = 400 mcg : x ml
1000x = 2(400)
1000x = 800
x = 800/1000
x = 0.8 ml
ALWAYS write a zero in front of the decimal point to prevent errors *

Sample Problems

▪ 25 mg = x g
▪ 0.3 mg = x g
▪ 2.8 L = x ml
▪ 1000 mg : 1 mg = 150 mg : x mg
▪ 200 mg : 5 ml = 300 mg : x ml
▪ 175 mcg : 1 tab = 350 mcg : x tab

▪ Ordered : Vistaril 60 mg
▪ Available : Vistaril 100mg/2ml

▪ Ordered : Heparin 2000u
▪ Available : Heparin 6000u/ml

▪ 20 mg is equal to how many gr?
60 mg : 1 gr = 20 mg : x gr
60 x = 20/60 = (1/3)
x = 0.333

▪ 1/4 tsp equals how many milliliters?
1 tsp : 5 ml = 1/4 tsp : x
1x = 5/4
x = 1.25

▪ 0.04 g = ____μg
1 g : 1000mg = 0.04 g : x mg
x = 40 mg
1 mg : 1000 μg = 40 mg : x μg
x = 40,000

▪ gr 1/6 = ____mg
1 gr : 60 mg = 1/6 : x mg
x = 60/6
x = 10 mg

Questions?