Composition of Functions
We have seen that functions can be combined by addition,
subtraction,
multiplication, and division. We now investigate a new way to combine functions.
We call it composition of functions. Composition of functions can give us an
equation that allows us to eliminate steps when calculating. A composition
uses the output of one function as the input of another function.
Let's review what a function is.
We can think of a function as a machine taking inputs and following some
rule, then returning an output. So we can keep track of these inputs and
outputs for a given function. Let's choose g(x) = 2x.
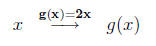
With a composition of functions we use the output of one
function as the
input of another function.
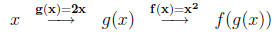
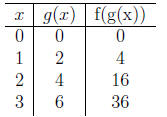
Let's examine the final outputs when f(x) = x^2
Example 0.1. Suppose the population P of a certain
species of fish depends on the number x (in hundreds)
of a smaller kind of fish which serves as its food supply,
so
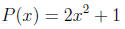
Suppose, also, that the number (in hundreds) of the
smaller species of fish depends on the amount a
(in tons) of its food supply, plankton, and
f(a) = 3a + 2.
Find P(f(a)) and interpret what it tells us.
a tells us the amount of plankton in the given area.
f(a) = 3a + 2 tells us how many of the small fish species should be in an
area that contains the amount a of plankton.
P(x) tells us the number of large fish as a function of the number of small
fish x
So P(3a+2) tells us the number of large fish based on the amount of plankton.
Let's look at this another way.
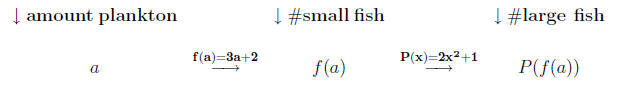
What is the formula for P(f(a))?
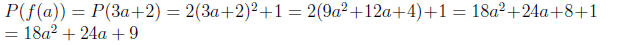
So if there are a tons of plankton in an area, we expect
to find 18a^2+24a+9
hundreds of large fish.
If there are 2 tons of plankton then we expect to find 18(2)^2+24(2)+9 = 129
hundreds of large fish.
Definition 0.1. The composition of the function f
with g is denoted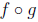 
and is defined by the
equation
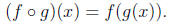
The domain of the composite function is the set of all x
such that
1. x is in the domain of g and
2. g(x) is in the domain of f.
Example 0.2. Find the domain of f(g(x)).
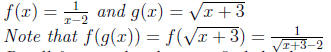
Recall from earlier how we find the domain.
1. x is in the domain of g
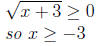
2. and g(x) is in the domain of f when
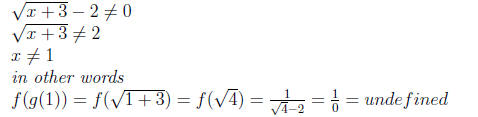
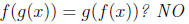
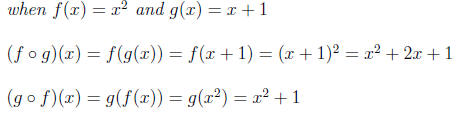
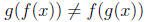Example 0.3. Is 
also the domain of
g(f(x)) is all real numbers.