M316 Final Exam
Name
This is a closed book, closed note exam. It consists of 8 problems, plus
3 extra credit problems. Each problem is worth 12 points, and each extra
credit problem is worth 3 points. In addition, you will receive 4 points
for writing your name. You may not use a calculator on this exam. Good luck!
1. Alexandra's used car lot is offering an additional 15% o cars that are
already 20% o the original price. Meanwhile, Mira's used car lot is
advertising 35% o the original price for all the cars on the lot. If the
car you want is available at both places (at the same original price),
where should you go and why? How much will you save by going to
the one used car lot as opposed to the other?
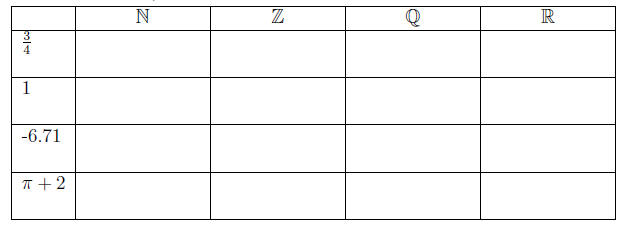
2. (a) Which of the numbers below are natural numbers? Which are
integers? Rational numbers? Real numbers? Fill in the chart
below by writing "yes" if the number belongs to the corresponding
set, and "no" if not. (Note: a number may belong to more than
one of these sets.)
(b) What is the additive inverse of -5? Why?
(c) There is one rational number that does not have a multiplicative
inverse. What is it? Why doesn't this number have a multiplicative inverse?
(d) Write a word problem that corresponds to this arithmetic problem:
(-6) (-2/3 ).
3. (a) Write the number 81 in base 6.
(b) Write the number 1035 in base 10 (recall that the subscript 5
indicates that the number is currently written in base 5).
(c) Do the following base 5 arithmetic problem: 300012425×215. (You
may leave your answer in base 5.)
4. (a) Peter is just beginning to learn to count using our
base 10 enumerative system.
He doesn't understand why 30 is the next number
after 29. How would you explain it to him?
(b) Which of the four fundamental operations of arithmetic
satisfy
the commutative property?
(c) What is 200,000 + 600,000?
(d) What is 21+43?
(e) Recall the distributive property of multiplication: if a, b, and c are numbers, then a(b + c) = ab + ac. In your solutions to problems (c) and (d) above, you implicitly used this property. Explain how.
5. (a) Determine the prime factorization of 231.
(b) What is the smallest number with 7 factors? What is
the smallest
number with 6 factors?
(c) Haley's comet can be seen every 75 years. The
Swift-Tuttle comet
can be seen every 135 years. If one year we see them both at the
same time, how long will it be before they are both visible in the
same year again?
6. For each of the four problems below, select the model
from the list that
ts. After brie y justifying your choice, solve the problem.
| Models: | + Combine, increase - Take-away, comparison, missing addend ×Repeated addition, area, Cartesian product 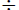 Partitioning, repeated subtraction,
missing factor |
(a) Julia is preparing a meal. She knows how to cook 13 different
entrees and 17 different side dishes. If a meal is a combination
consisting of one entree and one side dish, how many different
possible meals can Julia cook?
(b) In Portland, Maine, it was -11 degrees Farenheight on December
21st. After 8 days, the temperature warmed up to -5 degrees
Farenheight. How much warmer was it in Portland on December
29th than it was on December 21st?
(c) My car has an average fuel efficiency of 43 miles per gallon. If I
can travel 417.1 miles on a tank of gas, how large (in gallons) is
my gas tank?
(d) One day, Elizabeth decides to walk home from the office. If the
total distance from her office to her home is
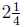miles, and she has
walked 2/3 of the way, how far away from the office is she?
7. (a) On Josh's birthday, his mom cuts his birthday cake into 6 pieces
and gives him 1. On Sammy's birthday, his mom cuts his cake
into 12 pieces and gives him 2. Josh begins to cry because Sammy
got more pieces of cake on his birthday than Josh got on his. How
would you explain to Josh that he actually got the same amount
of cake as Sammy?
(b) On Jerry's birthday, his mom cuts his birthday cake into 20 pieces
and gives him 3. Now Sammy is crying because Jerry got more
pieces of birthday cake than he did. How would you explain to
Sammy that he actually got more cake than Jerry did?
(c) Now that Sammy knows that he got more cake than Jerry, he
wants to know how much more. Determine how much more cake
Sammy got than Jerry, and then describe how you would explain
your solution to Sammy.
8. Let a; b be two numbers such that 0 < b < a < 1. In the table below,
fill in the second column with either <, = or > so that the first three
columns give a true number sentence. In the fourth column, give a
justification for your choice of <, =, or >. (Note: examples do not
constitute sufficient justification and will not receive full credit.)
Extra Credit: What is your instructor's favorite number?
Extra Credit: What is the last digit of 9100?
Extra Credit: Write the following rational number
in the form a/b ,
where a and b are integers: 0.027027027027027 …