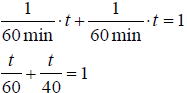RATIONAL EXPRESSION REVIEW

A rational expression is a fraction in which the numerator or denominator is a
variable expression (such as a polynomial).

A rational expression is in SIMPLEST form when the numerator and denominator
have no comman factors other than 1.

Reducing to simplest form – factor the numerator and denominator, then cancel out
any common factors in the numerator and denominator (not common factors that are
both in the numerator or both in the denominator, e.g. side by side).

Multiplying Rational Expressions – factor the numerators and denominators then
cancel out common factors as above, then multiply the numerators and multiply the
denominators.

Dividing Rational Expressions – change to a multiplication problem by changing
the DIVISOR into it’s RECIPROCAL.

Adding and Subtraction Rational Expressions –

Step 1:Factor the denominators, then find the LCM. The LCM of two polynomials is
the simplest polynomial that contains the factors of each polynomial. To find the
LCM of two or more polynomials, first factor each polynomial completely. The
LCM is the product of each factor the great number of times it occurs in any one
factorization.

Step 2: Change each rational expression so that the new denominator will be the
LCM. You will multiply tne numerator and denominator of each expression by
whatever it takes to get the LCM as the new denominator.

Step 3: Add the two new fractions by adding the numerators and keeping the
denominator (the LCM) the same.

Step 4: Now factor the resulting expression and cancel out any common factors in the
numerator and denominator.

Simplify Complex Fractions – Complex fractions are just rational expressions with
fractions within fractions. To simplify, find the LCM of all the denominators of
every fraction in the expression, then multiply the main numerator and denominator
by that LCM. Then simplify as usual.

Solving Equations with Fractions – multiply BOTH SIDES of the equation by the
LCM of all denominators in the equation. Then solve as usual.

If the equation is one fraction set equal to another, this is called a PROPORTION.
Solve by CROSS-MULTIPLYING, then isolating the variable.

APPLICATIONS OF RATIONAL EXPRESSIONS

Similar Triangles

Triangles are similar if at least 2 corresponding angles are the same
in each triangle.

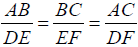
WORK

Rate of Work * Time Worked= Part of Tasked Completed

If someone can do a job in 60min, their rate of work is 1/60min.
If someone else can do the same job in 40minutes, their rate of work
is 1/40min.

The TIME to get the same job done TOGETHER can be found by
Adding their parts together to make 1 whole job.