Algebra II
| Idaho Department of Education | Objective | Sub Objectives | Task Analysis | Essential Vocabulary |
| Content Standards | ||||
| Cognitive level codes: • B: Memorize • C: Perform procedures • D: Demonstrate understanding • E: Conjecture, generalize, prove • F: Solve non-routine problems, make connections |
Bloom's Equivalent • B = Knowledge • C = Comprehension • D = Comprehension • E = Application and Analysis • F = Synthesis |
Calculator codes: • NO: student MUST NOT have a calculator while completing this item in order to assess this objective. |
||
| Standard 1: Number and Operation | ||||
| Goal 1.1: Understand
numbers, ways of representing numbers, relationships among numbers, and number systems. |
AII.1.1.1 Compare and contrast the
properties of numbers and number systems within the complex number system to include rational, irrational, and imaginary numbers and factorials. |
• Compare and contrast the properties
of numbers and number systems within the complex number system to include rational, irrational, and imaginary numbers and factorials. |
• Define and explain the meaning of i
s a solution to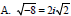 the equation x² = -1. - The square root of -1 is the basis of the imaginary number system. • Identify expressions of the form a + bi as complex numbers. - Every real number, a, is a complex number expressed as a + 0i. - Identify the real element and the imaginary element of a complex number. • Divide complex numbers using conjugates. • Demonstrate the meaning of x! - Evaluate factorials with and without calculators. |
• real number • imaginary number •
complex number • conjugates • factorial |
| AII.1.1.2 Demonstrate meaning of
complex numbers as solutions to polynomial equations that do not have real solutions. |
• Demonstrate meaning of complex
numbers as solutions to polynomial equations that do not have real solutions. |
• Identify real and imaginary roots
for polynomial equations. - Simplify those roots with negative radicands |
• radicand • roots | |
| AII.1.1.3 Recognize matrices as a
method of arranging data. |
• Recognize matrices as a method of arranging data. | • Identify the dimensions of a matrix. | • matrix • row • column | |
| AII 1.1.4 Develop an understanding of
the properties of logarithmic expressions and expressions with rational exponents. |
• Develop an understanding of the
properties of logarithmic expressions and expressions with rational exponents. |
• Identify a logarithmic function as
the inverse of an exponential function. - Identify logarithmic and exponential functions graphically. - Define e. • Apply the laws of exponents to algebraic expressions, including those involving rational and negative exponents, to order and rewrite them in alternative forms. - i.e. 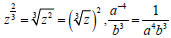 |
• inverse function • logarithmic
function • exponential function • logarithm base • rational exponent |
|
| Goal 1.2: Understand meanings of operations and how they relate to one another. |
AII 1.2.1 Develop an understanding of
the properties of, and representations for, the addition, subtraction, and multiplication of matrices. |
• Develop an understanding of the
properties of, and representations for, the addition, subtraction, and multiplication of matrices. |
• Identify which properties of real
numbers apply to matrices. |
|
| Goal 1.3: Compute
fluently and make reasonable estimates. |
AII.1.3.1 Simplify expressions within
the complex number system. |
• Simplify expressions within the
complex number system. |
• Simplify rational expressions,
expressions with rational exponents, and logarithmic expressions. - Simplify rational expressions containing monomials in the numerator and denominator. - Simplify rational expressions that contain polynomials in the numerator and denominator that require factoring. - Simplify complex fractions. • Simplify and estimate radical expressions having various indices. • Express the square root of a negative number in the form bi, where b is real. • Simplify rational expressions containing complex numbers. • Use properties of logarithms to simplify logarithmic expressions. - Expand single logarithmic expressions. - Write expanded logarithmic expressions as single logarithmic expressions. - Apply change of base formula to convert a logarithmic expression to an appropriate base. |
• indices • rational exponent •
rational expression • logarithm • complex fraction |
| AII 1.3.2 Perform computations on
expressions within the complex number system. |
• Perform computations on expressions
within the complex number system. |
• Perform operations with matrices to
include scalar multiplication, addition, subtraction, and matrix multiplication (2 by 2). • Add, subtract, and multiply radical expressions and expressions containing rational exponents. • Use long division or synthetic division to divide a polynomial by a lower degree polynomial. • Add and subtract rational expressions with and without common denominators. • Multiply and divide rational expressions. - Recognize the difference between a factor and a term when simplifying rational expressions. |
• scalar • radical expression •
synthetic division • degree of a polynomial • factors • terms • like radical expressions |
|
| Standard 2: Concepts and Principles of Measurement | ||||
| Goal 2.1: Understand
measurable attributes of objects and the units, systems, and processes of measurement. |
AII.2.1.1 Recognize the
relationship between radian and degree measures. |
• Recognize the
relationship between radian and degree measures. |
• Convert between degree and radian measures. | • degree • radian |
| Goal 2.2: Apply appropriate techniques, tools,, and formulas to determine measurements. |
No objectives at this course level. | |||
| Standard 3: Concepts and Language of Algebra and Functions | ||||
| Goal 3.1: Understand
patterns, relations, and functions. |
AII.3.1.1. Represent patterns and
functional relationships in a table and as a graph. |
• Represent patterns and functional
relationships in a table and as a graph. |
• Graph absolute value functions. • Graph quadratic equations and inequalities. • Graph polynomial functions. - Determine end behavior and x- and y-intercepts. • Graph exponential functions. • Graph circles. - Identify the coordinates of the center and determine the length of the radius. • Graph functions by plotting points. • Determine domain and range using algebraic and graphing techniques. |
• absolute value function • quadratic
function • domain • range • end behavior |
| AII.3.1.2. Describe the graphs of
polynomial and absolute value functions and discuss their attributes in terms of the basic concepts of maximum, minimum, intercepts, and roots. |
• Describe the graphs of polynomial
and absolute value functions and discuss their attributes in terms of the basic concepts of maximum, minimum, intercepts, and roots. |
• Determine the nature of the roots
of an equation by using the discriminant. • Recognize contexts in which quadratic models are appropriate. - i.e. height as a function of time; the relationship between the length of a side of a cube and its surface area. • Identify the graphs of absolute value functions and identify their key characteristics. • Determine the degree of a polynomial function. • Determine the vertex and axis of symmetry of a quadratic function. • Identify the graphs of polynomial functions. -i.e. parent graphs • Find the x- and y-intercepts for applicable functions. |
• x- and y-intercepts • zeros •
discriminant • polynomial function • parent graph • vertex • axis of symmetry |
|
| AII 3.1.3. Perform operations on
functions including composition of functions and finding inverse functions. |
• Perform operations on functions
including composition of functions and finding inverse functions. |
A. Combine functions by addition,
subtraction, multiplication, and division. B. Determine the composition of two functions, including any necessary restrictions on the domain. C. Determine and graph the inverse relation of a function. - Determine if the inverse relation is a function. |
• composition of functions • inverse
relation • inverse function |
|
| Goal 3.2: Represent and
analyze mathematical situations and structures using algebraic symbols. |
AII.3.2.1. Write equations and
inequalities in multiple forms. |
• Write equations and inequalities in multiple forms. | • Rewrite equations of parabolas and
circles in standard form by completing the square as necessary. - i.e. Use different forms of the function to extract information For parabolas: y = x² - 6x + 8 makes the y-intercept obvious, y = (x - 2)(x - 4) provides access to the zeros, and y = (x - 3)² - 1 makes it easy to find the vertex and sketch the graph. |
• perfect square trinomial • complete the square |
| AII.3.2.2. Recognize and generate
equivalent forms of algebraic expressions and solve equations, inequalities, and systems of equations and inequalities. |
• Recognize and generate equivalent
forms of algebraic expressions and solve equations, inequalities, and systems of equations and inequalities. |
• Solve systems of linear equations
by graphing and algebraic processes. - Determine the number of solutions for a system of equations. • Solve systems of linear inequalities by graphing. • Determine if an ordered pair satisfies a system of linear equations or inequalities. • Solve radical equations and inequalities. - Determine the domain and range of radical equations. - Determine if extraneous solutions exist. • Solve rational equations. - Determine the domain and range of rational equations. - Determine if extraneous solutions exist. • Solve logarithmic equations. • Solve equations containing a variable in the exponent. • Use the quadratic formula, factoring, and completing the square to solve quadratic equations. • Determine a single variable quadratic equation given its solutions. |
• systems of equations • radical
equations • extraneous solutions • quadratic formula |
|
| Goal 3.3: Use mathematical models to represent and understand quantitative relationships. |
No objectives at this course level. | |||
| Goal 3.4: Analyze change in various contexts. |
AII.3.4.1. Interpret how changes to
an equation effect the parent graph of the equation. |
• Interpret how changes to an
equation effect the parent graph of the equation. |
• Compare and contrast the graphs of f(x) = x² to f(x) = a(x-h)² + k. • Recognize graphs of the following: 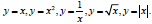 • Identify vertical and horizontal translations and reflections about the x-axis. |
• translation • reflection |
| Standard 4: Concepts and Principles of Geometry | ||||
| Goal 4.1 Analyze characteristics and properties of two- and threedimensional geometric shapes and develop mathematical arguments about geometric relationships. |
AII.4.1.1 Use trigonometric
relationships to determine lengths and angle measures. |
• Use trigonometric relationships to
determine lengths and angle measures. |
• Solve right triangles using the
Pythagorean theorem and trigonometric ratios. • Demonstrate the proper use of the Law of Sines and the Law of Cosines to solve triangles. |
|
| Goal 4.2 Specify locations and describe spatial relationships using coordinate geometry and other representational systems. |
AII.4.2.1. Analyze the graphs of circles and parabolas. | • Analyze the graphs of circles and parabolas. | • Graph circles and parabolas and their transformations. | |
| Goal 4.3 Apply transformations and use symme |
No objectives at this course level. | |||
| Goal 4.4 Use visualization, spatial reasoning, and geometric models to solve problems. |
No objectives at this course level. | |||
| Standard 5: Data Analysis, Probability, and Statistics | ||||
| No objectives at this course level. | ||||


