Crash Introduction to Quantifiers

This lecture finishes the quick introduction to quantifiers, which follows
part of section 1.3 of Rosen. We’ll also see some examples of direct proof,
from section 1.6 of Rosen. Don’t worry about reading either section right
now. We’ll do that when we’re closer to covering their full content.

1 Announcements

Turn in your homework: please put it in the folder for your section on the
back table.

Announcement from Fernanda Mendes about the UIUC WCS (“Women
in Computer Science”) mentoring program. Match you up with corporate
mentors. Open to everyone (not just women). Details on their web site.

2 Recap

Recall from last lecture that a predicate (e.g. x² ≥ 0) is a statement that
becomes true or false when you substitute particular values for its variables
(e.g. 3² ≥ 0). Predicates are used to make general claims about whole sets
of values, such as “For every integer x, x² ≥ 0.” Notice that we carefully
specified the type of x, i.e. what types of values (integers in this case) that
we allow to be substituted for the variable x. The set of values that can be
substituted in for a variable is called its domain or its replacement set.

3 Quantifiers

The operation “for all x” is formally known as a universal quantifier.

The other heavily-used quantifier in formal mathematics is the existential
quantifier, written “there exists an x” For example, “there exists an integer x
such that 5 < x < 100.” This means that at least one integer x (and possibly
a whole bunch of integers) satisfies the equation.

Notice that the existential quantifer is followed by “such that” in fluent
mathematical English, which isn’t quite parallel to what you see with the
universal quantifier. This isn’t for any good reason. It’s just how math-
ematical English happens to have evolved, and you should do likewise so
that your written mathematics looks professional. “Such that” is sometimes
abbreviated “s.t.”

The general idea of a quantifier is that it expresses express how many of
the values in the domain make the claim true. Normal English has a wide
range of quantifiers which tell you roughly how many of the values work,
e.g. “some”, “a couple”, “a few”, “many”, “most.” Mathematics largely
uses just the two we’ve seen, though you occasionally see a third quantifier
“there exists a unique x.” This means that one and only one x satisfies the
predicate. For example, “there is a unique integer x such that x² = 0.”
Mathematicians use the adjective “unique” to mean that there’s only one
such object (similar to the normal usage but not quite the same).

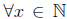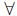In a statement like , x ≤ 2x, the quantifier is said to “bind”
its variable x. Similarly, summations and integrals bind their dummy
variables, e.g. the i in 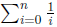. Variables that aren’t bound are called “free.”
Statements containing free variables don’t have a defined truth value.

4 Shorthand notation

The universal quantifier has the shorthand notation 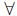. For example, 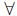x ∈ N, x ≤ 2x.
The existential quantifier is written 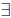, e.g. 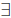y ∈ Ry = √2. Notice
that we don’t write “such that” when the quantifier is in shorthand. The
unique existence quantifier is writte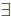n ! as in 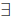!x ∈ R, x^2 = 0

There’s several conventions about inserting commas after the quantifier
and/or parentheses around the following predicate. The style in these notes
and the style in Rosen are both ok to copy from.

If you want to state a claim about two numbers, you can use two quantifiers as in:

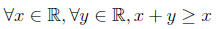
This is usually abbreviated to

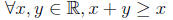
This means “for all real numbers x and y, x + y ≥ x” (which isn’t true).
When manipulating 2D points, you have several options. You can write
something like x, y ∈ Z (“for any integers x and y”) and then later refer to
the ordered pair (x, y). Or, people also write 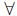(x, y) ∈ Z² (“For any point
(x, y) with integer coordinates”). Or you can write something like 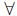p ∈ Z²
(“for any 2D point p with integer coordinates”). Then, when you later need
to access its two coordinates, you can assert (based on our knowledge of 2D
geometry) that p has the form (x, y), where x and y are integers. All three
approaches work ok.

5 Negating statements with quantifiers

In general, a statement of the form “for all x in A, P(x)” is false exactly when
there is some value x in A such that P(x) is false. In other words, when “there
exists x in A such that P(x) is not true”. In shorthand notation:

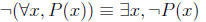
Similarly,

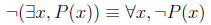
So this is a bit like the de Morgan’s laws: when you move the negation
across the operator, you change it to the other similar operator.

Last class, we saw how to move negation operators from the outside to the
inside of expressions involving ∧, ∨, and the other propositional operators.
Together with these two new rules to handle quantifiers, we now have a
mechanical procedure for working out the negation of any random statement
in predicate logic.

So if we have something like

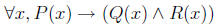
It’s negation is

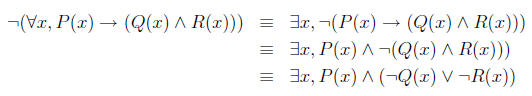
6 Proving a universal statement

Now, let’s consider how to prove a claim like
For every rational number q, 2q is rational.

First, we need to define what we mean by “rational”.
A real number r is rational if there are integers m and n, n ≠ 0, such
that r = m/n .

The simplest technique for proving a claim of the form x ∈ A, P(x) is
to pick some representative value for x. Think about sticking your hand
into the set A with your eyes closed and pulling out some random element.
You use the fact that x is an element of A to show that P(x) is true. Here’s
what it looks like for our example:

Proof: Let q be any rational number. From the definition of
“rational,” we know that q = m/n where m and n are integers and
n is not zero. So 2q = 2m/n = 2m/n . Since m is an integer, so is
2m. So 2q is also the ratio of two integers and, therefore, 2q is
rational.

At the start of the proof, notice that we expanded the word “rational”
into what its definition said. At the end of the proof, we went the other
way: noticed that something had the form required by the definition and
then asserted that it must be a rational.

Notice also that we spelled out the definition of “rational” but we just
freely used facts from high school algebra as if they were obvious. In general,
when writing proofs, you and your reader come to some agreement about
what parts of math will be considered familiar and obvious, and which require
explicit discussion. For this course, basic facts from high school math courses
will be considered obvious.

7 A couple notational issues

WARNING!! Abuse of notation. Notice that our definitions said “if”.
If you take them literally as read, that means you can only use them in one
direction. This isn’t what’s meant. Definitions are always intended to work
in both directions, i.e. I meant to say “if and only if.” This little misuse of
“if” in definitions is very, very common.

Also notice that “iff” is shorthand for “if and only if”, which is the same
thing as ↔.

8 Proving existential statements

Here’s an existential claim:

Claim 1 There is an integer k such that k^2 = 0.

An existential claim such as the following asserts the existence of an object
with some set of properties. So it’s enough to exhibit some specific concrete
object, of our choosing, with the required properties. So our proof can be
very simple:

Proof: Zero is such an integer. So the statement is true.

We could spell out a bit more detail, but it’s really not necessary. Proofs
of existential claims are often very short, though there are exceptions.

Notice one difference from our previous proofs. When we pick a value to
instantiate a universally quantified variable, we have no control over exactly
what the value is. We have to base our reasoning just on what set it belongs
to. But when we are proving an existential claim, we get to pick our own
favorite choice of concrete value, in this case zero.