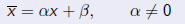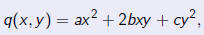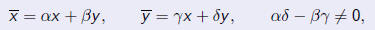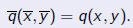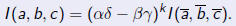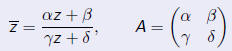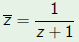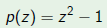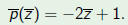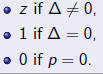Classical Invariant Theory Through an Example
Classical Invariant Theory
Classical invariant theory is the study of intrinsic properties of
polynomials.
By intrinsic, we mean those properties which are unaffected by a change of
variables and are purely geometric.
Intrinsic properties:
• factorizability,
• multiplicities of roots,
• geometrical configurations of roots.
Non-intrinsic properties:
• explicit values of the roots,
• particular coefficients of the polynomial
The study of invariants is closely tied to
the problem of equivalence:
• when can one polynomial be transformed into another by a suitable
change of coordinates.
the associated canonical form problem:
• find a system of coordinates in which the polynomial takes on a
particular simple form.
The first goal of classical invariant theory is to determine the fundamental invariants of polynomials.
George Boole
 |
(November 2, 1815 { December 8, 1864) was an English mathematician and philosopher. Inventor of Boolean algebra |
Arthur Cayley
 |
(August 16, 1821 { January 26, 1895) was a British mathematician. Proved the Cayley-Hamilton He was the first to define the |
David Hilbert
 |
(January 23, 1862 { February 14, 1943) was a German mathematician. Proved the Hilbert basis Invented Hibert spaces. |
Quadratic Polynomials
Disclaimer: All the considerations are over C
Let
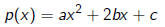
be a quadratic polynomial. As long as a ≠ 0, the roots are
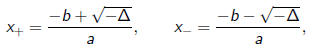
where
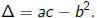
The existence of two roots implies that we can write
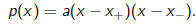
| Proposition |
| The affine transformation
preserves the class of quadratic polynomials |
An affine transformation sends a polynomial p(x) to a new polynomial
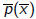 defined so that
defined so that
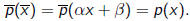
Say
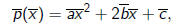
then
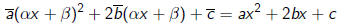
Expending we get
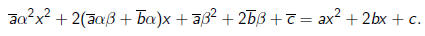
Hence
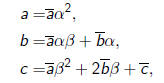
and
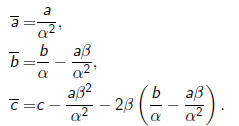
| Example |
Consider the polynomial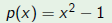 and the change of variable 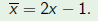 Then 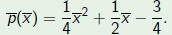 The roots 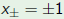 of p go to
of p go to
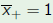 and and
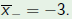 |
Canonical Forms
If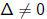 then p has 2 distinct roots. By translation we can shift x_
then p has 2 distinct roots. By translation we can shift x_
to 0, then by (complex) dilation we can make x+ to be equal to 2i .
Then we can shift the complex plane by -i . Hence a canonical
polynomial is
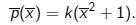
If 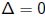 then p has a double
root x0. We can translate x0 to 0, thus
then p has a double
root x0. We can translate x0 to 0, thus
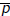 is a multiple of
is a multiple of
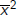 . By scaling we can reduce the multiple to 1.
. By scaling we can reduce the multiple to 1.
Hence the canonical form is
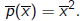
| Proposition |
| The affine canonical forms for complex
quadratic polynomials are
|
Quadratic Forms
| Definition |
| The homogeneous quadratic polynomial
in two variables x, y is called a quadratic form. |
To every quadratic form we can associate the polynomial
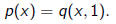
Inversely, a polynomial p(z) induces a quadratic form
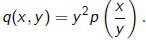
| Theorem |
| Any invertible change of variables of the form
maps a quadratic form to a quadratic form according to
|
Let
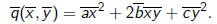
The coefficients 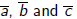 are
related to the coefficients a, b, and c of
are
related to the coefficients a, b, and c of
q(x, y) by the relations
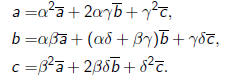
| Definition |
| An invariant of a quadratic form q(x, y)
is a function I (a, b, c), which, up to a determinantal factor, does not change under a general linear transformation:
The determinantal power k is called the weight of the invariant |
| Theorem |
| The discriminant is an invariant of weight two: |
| Remark |
| Our classification of quadratic polynomials is
based on the fact that = 0 or 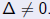 . From (1), if . From (1), if
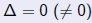 then it stays equal (not equal) to
zero then it stays equal (not equal) to
zerounder a change of variables |
Projective Transformations
Recall that
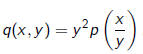
Thus the transformation
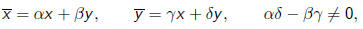
induces the transformation
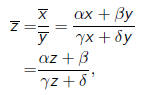
where z = x/y.
| Definition |
| The transformation
is called a linear fractional or MÖbius or projective transformation. |
This simple transformation is of fundamental importance in
•projective geometry,
•complex analysis and geometry,
•number theory,
•hyperbolic geometry.
A linear fractional transformation induces a
transformation on quadratic
polynomials defined by
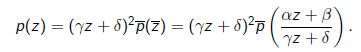
The transformation rules for the coefficients of a quadratic polynomial are
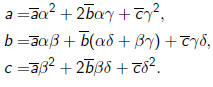
| Example |
| The inversion
maps the quadratic polynomial
to
Thus projective transformations do not necessarily preserve the degree of a polynomial. |
Canonical forms
Let p(z) be a quadratic polynomial. We can assume it is in one of the affine canonical forms.
1) Let p(z) = k(z^2 + 1). If we scale according to the coefficient matrix
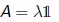
such that λ^2 = k then
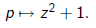
Under the transformation
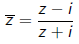
the polynomial z^2 + 1 goes to
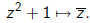
2) Let p(z) = z^2 then under the inversion
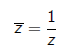
it is mapped to
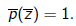
| Proposition |
| The canonical forms for complex quadratic
polynomials are
|
Generalizations
•Polynomials and forms of order greater than 2.
•Polynomials and forms with more variables (hardcore algebraic
geometry!).
•Work with polynomial rings over more general fields (hardcore
algebra!).
(Partially) Open Problems
1) The discriminant
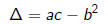
of a quadratic polynomial
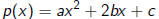
is an invariant and characterizes the multiplicity of the
roots (and the
canonical forms).
Question: If one considers polynomials of higher
degree or larger number
of variables, how many invariants, similar to the discriminant, are there?
What properties do they characterize?
2) Consider the binary form
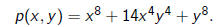
Any of the following four complex linear substitution
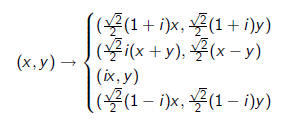
does not change the polynomial. p(x, y) is also invariant
under the group
they generate, consisting of 192 elements.
The binary form
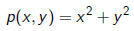
has infinitely many symmetries since it contains all
rotations in the
xy-plane.
The binary form
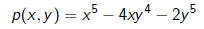
is preserved only by scaling by a fifth root of unity:
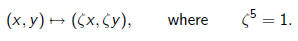
Question: Given a multivariable polynomial, how can
one efficiently find
the size of its symmetry group and compute it explicitly?
3) The transformation
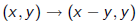
sends
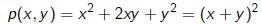
to
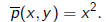
Note that the Hessian
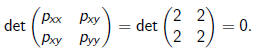
Fact: The Hessian of a homogeneous polynomial in 2
variables is zero if
and only if it can be transformed to a polynomial of a single variable by a
linear change of variables.
Hesse claimed a similar result was true for any number of
variables: A
homogeneous polynomial
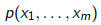
can be transformed to a polynomial of fewer than m
variables if and only if
its Hessian
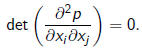
The conjecture was shown to be true by Noether and Gordan only for m≤4.
Question: How can one determine efficiently that a
given polynomial
essentially depends on a fewer number of variables than it seems to be?
How to find the corresponding change of variables.