Divide Polynomials

Math D: 6.4

There will be times when we wish to divide polynomials. This is done almost
the same way we divide integers, except that care must be taken to keep sep-
arate terms separate.

Property 0.1 To divide a polynomial by a monomial:

 1. Write the division as a fraction.
 2. Split the fraction with respect to 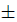in the numerator
 3. Reduce each fraction separately.

Example 0.1 Dividing by a polynomial

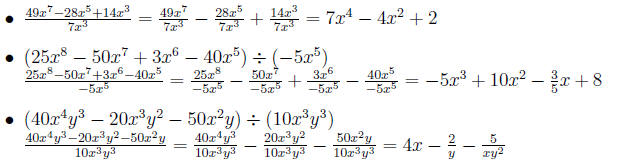
Sometimes we wish to divide by polynomial containing more than one term.
In this case we turn to polynomial long division.

Property 0.2 Long Division of Polynomials

 1. Arrange the terms of both the dividend and the divisor in descending powers of the variable.
 2. Divide the ¯rst term in the dividend by the ¯rst term in the divisor. The result is the ¯rst term in the quotient.
 3. Multiply every term in the divisor by the ¯rst term in the quotient. Write the resulting product beneath the dividend with like terms lined up.
 4. Subtract the product from the dividend.
 5. Bring down the next term in the original dividend and write it next to the remainder to form a new dividend.
 6. Use this new expression as the dividend and repeat this process until the remainder can no longer be divided. This will occur when the degree of the remainder (the highest exponent on a variable in the remainder) is less than the degree of the divisor.

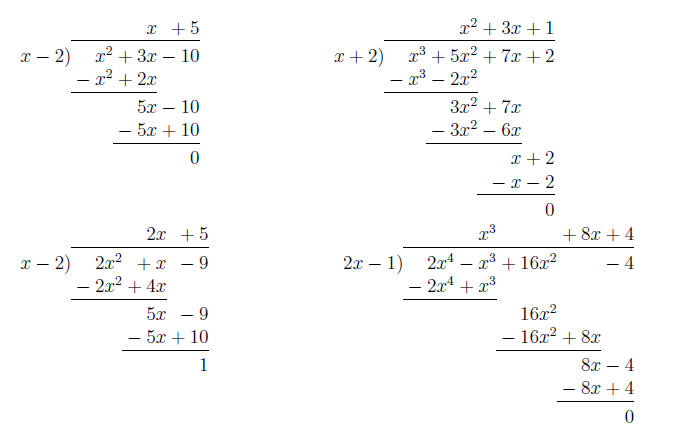
so the answer is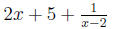

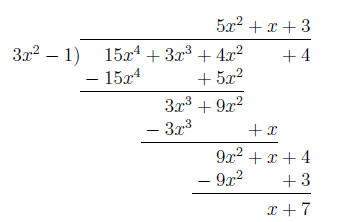
so the answer is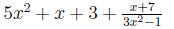.