Math 8 lecture notes
• We can extend the definition of logarithm to nonzero complex numbers z if
we accept
that it has to be a multivalued function. We called this multivalued function
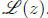
• Next we defined ab for any a, b ∈C, with a ≠ 0:
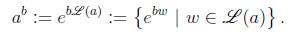
This is a set, meaning it could potentially have more than one value!
• This seems a little crazy at first, but it’s not so bad.
For example we saw that this
definition of ab as a set agrees with our intuition when b is a
rational number: if b = p/q
in lowest terms, then ab will consist of q different values (e.g., 361/2
= {−6, +6}).
• But this definition also has interesting consequences
when b is not a rational number: if
b is irrational, then ab will have infinitely many values! For
instance, if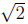 
= 1.4142...
is the positive square root of 2, then
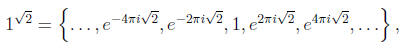
and these numbers are all different.
• I left it as an exercise to show that
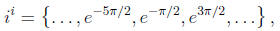
which is a little unexpected: it says that all values of
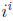are positive real numbers!
1