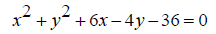Practice Test Three B

1. Completely factor the following expressions (3pts each):

2. Given the general quadratic equation ax^2 + bx + c = 0 , state the Quadratic Formula (3pts):

3. Use the method of COMPLETING THE SQUARE to solve the quadratic equations (4pts each)

4. Use the QUADRATIC FORMULA to solve the quadratic equations: (4pts each)

5. Without actually solving the equation, use the discriminant to discuss the nature of the roots of the following
quadratic equations (3pts each):

6. Solve the equation (do not check for extraneous solutions): (4pts)

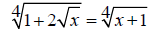
7. Solve the equation (do not check for extraneous solutions): (4pts)

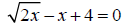
8. After doing everything correctly, Joe College
obtained x = 9/4 and x = 4 as solutions to the
equation 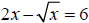. Determine which
solution(s) is (are) extraneous. (4pts)

9. After doing everything correctly, Joe College
obtained x = -5 and x = 3 as solutions to the
equation 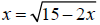. Determine which
solution(s) is (are) extraneous. (4pts)

10. Shade the area of the plane determine by the following inequalities: (2pts each)

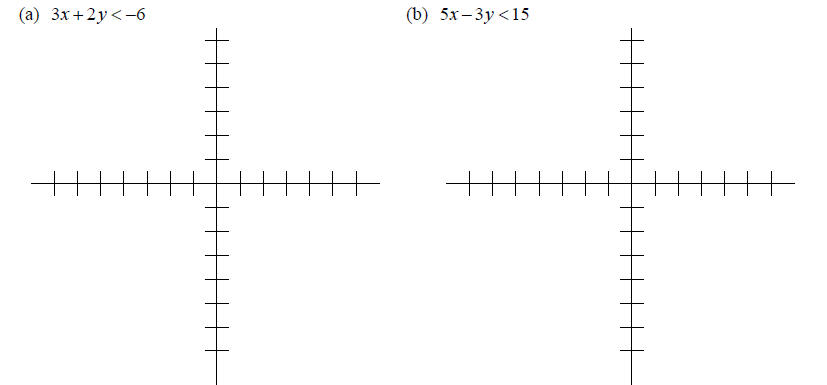
11. Solve the following systems of equations by using the SUBSTITUTION method (4pts each):

12. Solve the following systems of equations by using the ELIMINATION method (4pts each):

13. Determine an equation of a line which is parallel
to the line 2x + 3y = 27 and passing through the
point (3, -4). (4pts)

14. Determine an equation of a line which is
perpendicular to the line 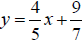and passing
through the point (-3, 5) . (4pts)

15. Determine an equation of the perpendicular bisector of the line segment whose midpoint is (−2,3) and has
slope = -7/4. (4pts)

16. Write an equation of a circle with center at. (3pts each)
(a) (3, 4) and radius of 5
(b) (–2, 5) and radius of 7

17. Determine the center and radius of each of the circles (3pts each)

18. Sketch the graph of the circle with center at (3, 2) and radius = 5. (3pts)

19. Determine the center and radius of the circle (5pts).