Level A Math Skills Assessment

A calculator is not allowed on the Level A Math Skills Assessment.

Decimal Addition and Subtraction
1) 19.017 + 2.88	2) 4.13 + 21.21
3) 30.69 - 29.18	4) 12.02 - 6.069

 

Decimal Multiplication and Division
1) 5.4 x 5.05	2) 0.6643 x 2
3) 20.8 x 6.1	4) 9.14 x 1.3
5) 11.2 ÷ 100	6) 7.035 ÷ 3
7) 3.82 ÷ 2	8) 4.131 ÷ 100

 

Order of Operations
1) Simplify the expression below. 12 - 6 • (5 + 23)	2) Simplify the expression below. 12 ÷ 6 • 42 - 12 + 2
3) Simplify the expression below. 2 • 7 + 33 - 4 ÷ 2	4) Simplify the expression below. 4 + 23 • (42 - 9)

 

Fraction Addition and Subtraction

 

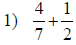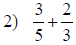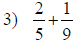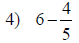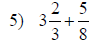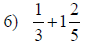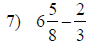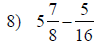Fraction Multiplication and Division

 

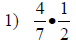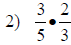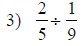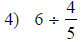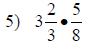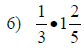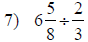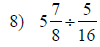Converting Fractions to Decimals and Percents
1) Convert 3/4 to a decimal and a percent.	2) Convert 4/5 to a decimal and a percent
3) Convert 3/8 to a decimal and a percent.	4) Convert 1/8 to a decimal and a percent.

 

Evaluating Expressions
1) Evaluate a - b(a - x)2 if a = -1,b = -2 and x = 3.	2) Find the value of a2b - 2a - 2cwhen a = -3,b = 4 and c = -5.
3) Find the value of 3a2 - 2bc + c2 when a = -3,b = 4 and c = -5.	4) Find the value of x/3 + 4x2 - 5y when x = -3, y = 2 .

 

Solving Equations
1) Solve for x: 5x - 2 + 3x = -26	2) Solve for x: 3(2x - 3) + 5 = 20
3) Solve for x: -7 = 3(2x +1)	4) Solve for x: 3(5x - 6) + 6 = 13
5) Solve for x: 7x - 8 = 2(3 + 2x) + 4	6) Solve for x: 2x/5 + 4 = -6
7) Solve for x: 10 + x/3 = 23	8) Solve for x: (1/2)x + 6 = 10

 

Solving Proportions

 

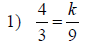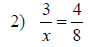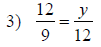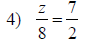Solving Inequalities
1) Solve: 14 ≥ 3x + 2	2) Solve: 2x - 4 ≥ - 2
3) Solve: 2(x - 4) - 3 > 21	4) Solve: 9 > 7 - 4x

 

Writing Expressions

1) Write an algebraic expression that represents “six less than half a number, x?”

2) Dawn is 3 years older than her sister Sara. If Dawn’s age is represented by x, which expression represents Sara’s age?

3) Cindy has four more than five times as many cousins as Kathy, k. Write an expression that represents how many cousins Cindy has compared with Kathy?

4) Sarah collects stamps and keeps them in envelopes. She had 9 envelopes with a certain number of stamps, s, in each envelope. She sells 3 of the envelopes. Find an expression that represents the number of stamps Sarah has left.

Problems Involving Fractions

1. Bonita bought 2(1/5) kg of potatoes and 1(1/2) kg of carrots. How much more potatoes than carrots did she
buy?

2. A carpenter made shelves of length 3(1/4)ft. and 3(1/8)ft. If his board was 8(1/2)ft long, how many feet of board
did he have left over?

3. From a piece of ribbon 12(1/2) inches long, a piece 5(3/4) inches long is cut. How many inches of ribbon are
left?

4. Joan’s room requires 20(1/4) square yards of carpeting and Sam’s room requires 17(7/8) square yards of
carpeting. How many more yards of carpeting does Joan’s room require?

5. To roast a turkey for Thanksgiving dinner, Juliette’s recipe calls for 3/4 of an hour cooking time per pound.
If her turkey weighs 12(1/2) pounds, how many hours should she cook her turkey?

6. About 1/3 of the land on the earth can be used for farming. Grain crops are grown on about 2/5 of this land.
What part of the earth’s land is used for growing grain crops?

7. Mrs. Meier had 3/5 kg of sugar. She used 1/4 of it to make cookies. How much sugar did she use to make the
cookies?

8. Natalie cuts a raffia 4(4/5)m long into 8 pieces of equal length. What is the length of each piece of raffia?
Give the answer in meters?

9. Four friends evenly split 6(1/2) liters of soda. How many liters of soda does each one get?

10. If 1/4 of a container holds 6 cups of water, how many cups of water does 1/8 of the same container hold?

11. The length of a page in a particular book is 8 inches. The top and bottom margins are both 7/8 inch. How
long is the page inside the margins, in inches?

12. Lauren spent 3/5 of her money on a refrigerator. The refrigerator cost $756. How much money had she left?

Problems Involving Percents

1. The Red Sox team played 160 games and won 65% of them. How many games did they win?

2. A basketball player took 400 shots during a season and scored on 40% of them. How many baskets did she
score?

3. A gasoline tank holds 20 gallons. If the tank is already 25% full, how many gallons of gasoline are needed
to fill the tank?

4. When the local department store put all of its shirts on sale for 20% off, Jason saved a total of $30 by
purchasing four shirts. What was the total price of the four shirts before the sale?

5. Twelve students participated in a science competition to represent Montana State University. If they are
15% of the total number of science majors, how many students are majoring in science at MSU?

6. If 6 feet of a 30-foot pole are underground, what percent of the pole’s length is above the ground?

7. Stacy won 8 of the 20 tennis games she played. What percent of the games did she win?

8. If 320 out of 500 families in a city have computers, what percentage of the families has computers?

9. Mr. Jenkins wants to distribute 40 fliers. He has distributed 30 fliers so far. What percent of the total
number of fliers has Mr. Jenkins distributed?

10. If 3/5 of John’s stamps are Canadian stamps, what percentage of his stamps are Canadian stamps?

Additional Problems

1. A certain recipe calls for 2 cups of milk for every 3 cups of flour. If 2 cups of flour are used, how many
cups of milk should be used?

2. Carlos burns 75 calories for every 15 minutes he walks. How many calories will Carlos burn if he walks
for 45 minutes?

3. Carlos burns 75 calories for every 15 minutes he walks. Carlos wants to burn 300 calories. How many
minutes must Carlos walk in order to burn 300 calories?

4. On the city map, 1 inch represents 1/2 mile. How many inches represent 3(1/4) miles?

5. Ellen buys 24 ounces of green beans at the grocery store. The green beans cost $1.90 per pound. How
much does she pay for the green beans, before tax? (1 pound = 16 ounces)

6. An art teacher mixes 20 ounces of yellow paint with 8 ounces of red paint. How many ounces of yellow
paint would she need to mix with 18 ounces of red paint to maintain the same proportion?