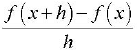Math 101 Review 1
Midterm 1
| Room | Sections | |||||
| Cat 061 | 022 | 025 | 029 | |||
| Matheson 109 | 014 | 015 | 028 | 030 | ||
| Nesbitt 111 | 010 | 012 | 013 | 027 | 031 | 033 |
Exam Coverage: 1.1-1.6
Date: Friday, February 1st 8-8:50 am
Recap of section 1.1:
Slope and equations of Lines:
Slope
Formula for slope: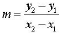 
1. Slope of a horizontal line is 0
2. Slope of a vertical line is undefined
Equations of Lines:
1. Use slope-intercept form (y = mx + b) if you are given
-The slope and the y-intercept
2.Use point-slope form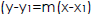 
if you are given
- The slope (m) and any point on the line,
- You are given two points on the line only (find the slope first, then pick a
point and use
point-slope form)
3. Equation of Horizontal line through the point (a, b): y = b
4. Equation of Vertical line through the point (a, b): x = a
Section 1.2
Properties of Exponents
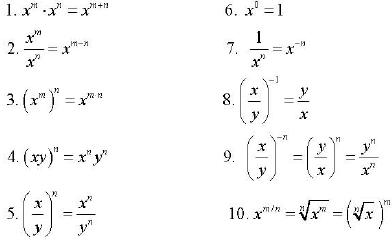(m/n: n is always the
root; you can then raise to the math power under or outside the
)
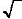1.3 Functions:
Domain and Range:
x = input value = independent variable; domain describes allowable values for x;
f(x) = y = output value = dependent variable; range describes possible output
for f(x)
The Vertical Line Test:
A curve in the Cartesian plane is the graph of a function if and only if, if no
vertical line intersects the
curve at more than one point.
Types of Functions:
Linear Function: A linear function is a function that can be expressed in the
form f(x) = mx +b with
constants m and b. Its graph is a line with slope m and
y-intercept b.
Quadratic Functions:
A quadratic function is a function that an be expressed
in the form
f(x) = ax2 + bx +c
with coefficients , a≠0, b and c.
Its graphs is called a parabola
In the equation f(x) = ax2 + bx +c.
If a>0, the parabola opens up and has a minimum.
If a<0, the parabola opens up and has a maximum.
The minimum or maximum value of a parabola is called its
vertex.
To find the vertex of quadratic functions:
Again, the vertex is the highest or lowest point of a parabola. To find the
vertex of a parabola:
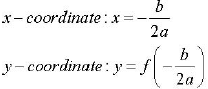
Solving Quadratic Equations:
A value of x that solves an equation f(x) = 0 is called a root of the equation
or the x-intercept of the
graph of y = f(x)
There are 2 methods to solve a quadratic equation:
• Factoring
To solve a quadratic equation, you must
1. Have the equation set = 0
2. Factor
3. Set each factor = 0 and solve for the variable
The solutions to ax2 + bx +c =0
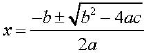
•Using the Quadratic Formula
Applications:
Profit, Revenue, and Cost:
Revenue: Revenue is the amount of money a company takes in from producing x
items.
Cost: The cost is how much it costs for the company to make the same x items.
Profit = Revenue – Cost A company breaks even if Revevue = Cost
Section 1.4 Functions Continued…
A Polynomial Function is a function that can be written in the form:
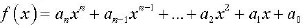
The domain is all Real numbers.
The degree is the highest power of the variable
Solving Polynomials:
Recall, solving means to find the value for the variable that makes the equation
true.
Have the equation set = 0
Factor
Set each factor = 0 and solve for the variable
Rational Functions:
A rational function is a fraction consisting of one polynomial divided by
another polynomial.
Domain: division by zero is undefined, so the domain of a rational function is
all real numbers, except
those which make the denominator 0.
Piecewise Linear Functions:
A piecewise linear function is a function which is given in several parts. For
example
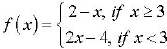
The Difference Quotient
