Solving Quadratic Equations
Solving Quadratic Equations
A quadratic equation is an equation of the form,
ax2 + bx + c = 0 ,
where a, b, and c are real numbers, with a ≠ 0 . The condition, a ≠ 0 , ensures
that the
equation actually does have a x2-term. When solving quadratic equations, we
consider
two cases: b = 0 and b ≠ 0 .
When b = 0, a quadratic equation is the form of ax2 − c = 0 so we use the square
root property to quadratic equations when b = 0.
Square Root Property
For any real number k, the equation x2 = k is equivalent to
.
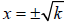If k > 0, then x2 = k has 2 real solutions.
k < 0, then x2 = k has no real solution.
k = 0, then 0 is the only solution to x2 = k .
Examples: Solving ax2 − c = 0
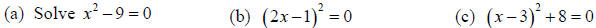
Solutions:
(a) Use the square root property to solve x2 − 9 = 0 .
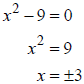
Thus, the solution set for the equation x2 − 9 = 0 is {-3, 3}.
(b) Using the square root property to solve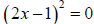
, we get
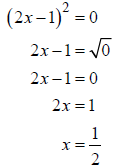
Thus, the solution set for the equation
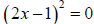is
.
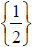(c) Use the square root property to solve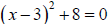 
.
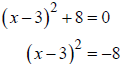
Because the square of any real number is nonnegative, the equation
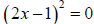
has no real solution.
For the case when b ≠ 0 , we can solve quadratic equations by factoring,
completing the square, and using the quadratic formula.
Solving Quadratic Equations by Factoring
Zero Factor Property
If A and B are algebraic expressions, then the equation AB=0 is equivalent to
the
compound statement A = 0 or B = 0.
Examples:
Solve the following quadratic equations by factoring.
(a) x2 − x −12 = 0
(b) (x + 3)(x − 4) = 8
Solutions:
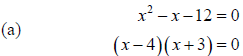
Using the zero factor property, we get
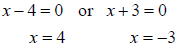
Thus, the solution set is {-3, 4} .
(b) (x + 3)(x − 4) = 8
First, multiply the left side using the FOIL method and subtract 8 from both sides.
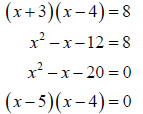
Using the zero factor property, we get
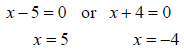
Thus, the solution set is {-4, 5} .
Solving Quadratic Equations by Completing the Square
To complete the square of x2 + kx , add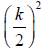 
to both sides. That is, add the
square of half the coefficient of x to both sides.
Examples:
Solve the following quadratic equations using completing the square
(a) x2 + 6x + 7 = 0
(b) 2x2 −3x − 4 = 0
Solutions:
(a) First, subtract 7 from both sides and then add
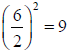to both sides:
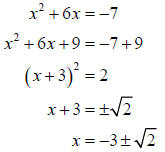
The solution set is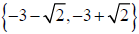 
.
(b) First, divide both sides by the leading coefficient, which is 2.
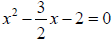
Now, add 2 to both sides and
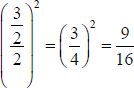to both sides.
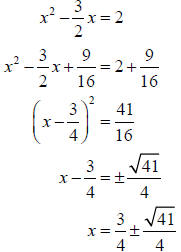
Thus, the solution set is
.
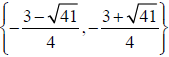Solving Quadratic Equations using the Quadratic Formula
Quadratic Formula
The solution to ax2 + bx + c = 0 , with a ≠ 0 , is given by the formula,
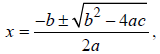
provided b2 − 4ac ≥ 0 . If b2 − 4ac < 0 , there are NO
REAL SOLUTIONS.
Example: Solve the quadratic equation, x2 + 8x + 6 = 0 , using the quadratic
formula.
Solution: Since a = 1, b = 8, and c = 6 ,
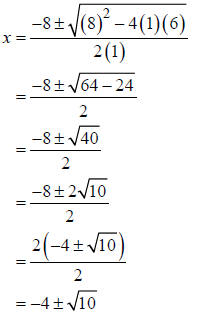
Thus, the solution set is
.
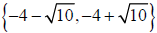