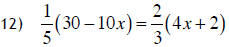Solving Linear Equations with the Variable on Both Sides of the Equation
This section uses the same tools as the previous section.
If you look at the steps, they are the same
except for step 4.
Steps to solving:
1) If fractions are present, multiply both sides of the equation by the LCD
(least common
denominator). After you are done multiplying by the LCD the equation will no
longer have
fractions.
2) Use the distributive property to remove parentheses.
3) Combine like terms that are on the SAME side of the equal sign.
4) Use the Addition Property to move all variable terms to the one side of the
equation and all
constant terms (numbers) to the other side of the equation. In this step you are
adding or
subtracting both sides of the equation by the same amount to move the term from
one side of
the equation to the other. It does not matter what side of the equal sign you
bring the variables
to and which one you bring the constants to. In your mind, make one side the
‘variable side’
and the other one the ‘constant side’. By the time you are done with this step,
the equation
will either look like ax=b (so proceed to step 5) OR the variables will cancel
out*.
*If the variables cancel out, look at what you are left with.
If you are left with a TRUE statement, then ALL REAL NUMBERS are solutions to
equation.
If you are left with a FALSE statement, then there is NO SOLUTION to the
equation.
5) Use the Multiplication Property to isolate the variable; that is, to get it
to look like x = # or
# = x. (It doesn’t matter on what side you isolate the variable.). This is
usually done by dividing
both sides of the equation by the coefficient.
6) Check the value you found by plugging it into the original equation. If you
get the same value
on both sides of the equal sign, the value you found is the solution to the
equation. If you get
different values, then the value you found is not a solution…look over your
work.
Examples: Solve.
1) 2x − 24 = 8x
2) −4m − 5 = 2m + 7
3) 12 − w = 2w + 9
4) 2.5x − 4.25 = 3x + 2.8
Now you: 5) 8 − 3x = 4x + 50
6) −4 + 2y = 2y − 6 + y
7) 21+ 2m = −2(m + 3) + 9
7) 2(x + 4) − 5 = −x − 6 + 3x + 9
Now you: 8) 4(x − 3) + 2 = 2x + 8

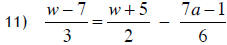
Now you: