Second Order Linear Equations
1. The Basic Types of 2nd Order Linear PDEs:
1.1. Generic and Standard Forms of 2nd Order Linear PDEs. The generic form of a
second
order linear PDE in two variables is
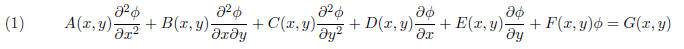
We shall see latter that by a suitable change of coordinates
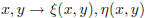we can cast any PDE of
the form (??) into one of the following three (standard) forms.
(1) Parabolic Equations:
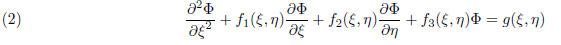
(2) Elliptic Equations:
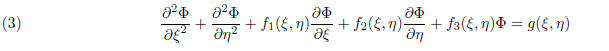
(3) Hyperbolic Equations:
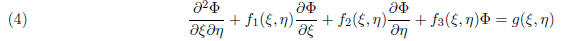
Associated to each of these standard forms are prototypical examples, each of
which also corresponds to a
fundamental PDE occuring in physical applications. For the next few weeks we
shall discuss the solutions
or each of these equations extensively.
1.2. The Heat Equation.
This equation arises in studies of heat flow. For example, if a 1-dimensional
wire is heated at one end, then
the function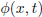 
describing the temperature of
the wire at position x and time t will satisfy (??). The
heat equation is the prototypical example of a parabolic PDE.
1.3. Laplace's Equation.
This equation arises in a variety of physical situations: the function
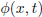might be interpretable as the
electric potential at a point (x, y) in the plane, or the steady state
temperature of a point in the plane.
Laplace's equation is the prototypical example of an elliptic PDE.
1.4. The Wave Equation.
This equation governs the propagation of waves in a medium, such as the
vibrations of a taunt string,
pressure fluctuations in a compressible fluid, or electromagnetic waves. The
wave equation is the prototypical
example of a hyperbolic PDE. The coordinate transformation that casts (7) into
the form (??) is
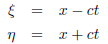
2. Boundary Conditions
In stark constrast to the theory of ordinary differential equations where
boundary conditions play a
relatively innocuous role in the construction of solutions, the nature of the
boundary conditions imposed on a
partial differential equation can have a dramatic effect on whether or not the
PDE/BVP (partial differential
equation / boundary value problem) is solvable.
2.1. Cauchy Conditions. The specification of the function and its normal derivative along the boundary curve.
Cauchy boundary conditions are commonly applicable in dynamical situations (where the system is interpreted as evolving with respect to a time parameter t:
2.2. Dirichlet Conditions. The specification of the function on the boundary curve.
As an example of a PDE/BVP with Dirichlet boundary conditions, consider the
problem of nding the
equilibrium temperature distribution of a rectangular sheet whose edges are
maintained at some prescribed
(but non-constant) temperature.
2.3. Neumann Conditions. The specification of the normal derivative of
the function along the
boundary curve.
As an example of a PDE/BVP with Neumann boundary conditions, consider the
problem of determining
the electric potential inside a superconducting cylinder.
3. Simple Solutions of the Heat Equation - Separation of Variables
In order to get a feel for the general nature of partial differential
equations, we shall now look for simple
solutions for the heat equation
We shall construct solutions of this equation by presuming the existence of
solutions of a particularly simple
(but sufficiently general) form. Our initial assumptions will be justified by
the fact that we obtain in this
manner lots of solutions.
Let us then suppose that there exist solutions of (8) of the form
where F is a function of x alone and G is a function of t alone. Substituting
this ansatz for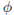 
into (8) yields
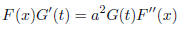
or
Now this equation should hold for all x and t. However, the left hand side
depends only on t while the right
hand side depends only on x. Consequently, if we vary t but keep x fixed, we
must have
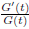equal to the
fixed number
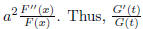equals some constant, say C. Similarly, by varying x and keeping t fixed
we can conclude that
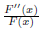is a constant as well, say D. Equation (10) then becomes
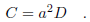
Thus, when we presume the existence of solutions of the form (9), the
diffusion equation (8) is equivalent
to the following pair of ordinary differential equations
Therefore, if we can construct solutions G and F of the ordinary differential
equations (4.1) and (4.1), then
(9) will be a solution of the partial differential equation (8). Rewriting (4.1)
and (4.1, respectively, as
We see that both of these ordinary differential equations are linear with
constant coefficients. The general
solution of (12a) will be
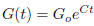
and the general solution of (12b) will have the form
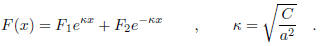
Thus, any function of the general form
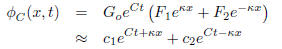
will be solutions of (8). Note that there are 3 undetermined parameters here,
C, c1 and c2. For fixed values
of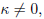 
, we obtain a two dimensional space of
solutions, since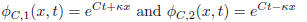 
are linearly independent. However, if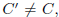 
then the functions
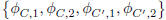are all linearly
independent.
If we take the separation constant C = k^2, with k real, we obtain
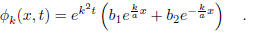
Varying c we thus obtain two 1-parameter families of
linear independent solutions whose magnitudes grow
exponentially in time:
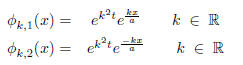
If we tak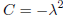e
, with λ real
constant, we have
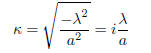
and so
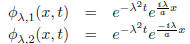
and
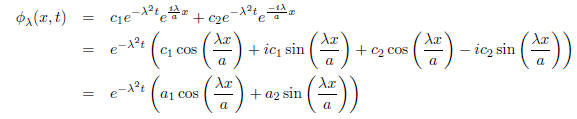
In the second step we have used Euler's formula
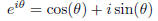
to replace the exponential functions
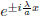by sine and cosine functions:
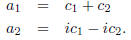
Varying λ we obtain two more 1-parameter families of
linearly independent solutions that decay exponentially as
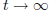, and oscillate sinusoidally as one varies x.
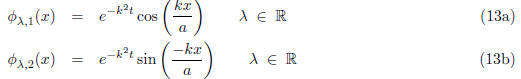
In summary, the method of separation of variables (i.e.,
the ansatz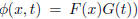 
produces four
1-parameter sets of linearly independent, real-valued solutions
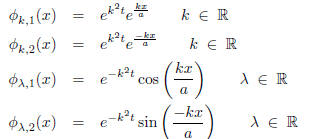
Given this plethora of linearly independent solutions, it
is appropriate to ask under what additional conditions
can we expect to find a unique solution. Clearly, specifying the value of
Φ at a single point will be
insufficient. We shall see latter that in order to obtain a unique solution we
will have to specify the values
of and its partial derivatives at every point along some curve in order to
completely determine a solution.