Algebra 2A
Credit By Exam Review Sheet
This Credit By Exam Review Sheet can help you prepare for the exam by giving
you an idea of
what you need to study, review, and learn. To succeed, you should be thoroughly
familiar with
the subject matter before you attempt to take the exam.
Every question that appears on the Credit by
Exam/Examination for Acceleration is grounded in
the knowledge and skills statements and student expectations within the
state-mandated
standards, the Texas Essential Knowledge and Skills (TEKS). It should be noted
that an exam
will not test every student expectation. However, it is important that students
study and know
the entire scope of the TEKS so that they can develop a complete understanding
of the content.
The CBE/EAs are a global exam grounded in the TEKS and are not designed to be a
final exam
for the University of Texas high school courses. You can view the TEKS for this
exam online at
Since questions are not taken from any one source, you can
prepare by reviewing any of the state-adopted textbooks.
About the exam
The Credit By Exam consists of 40 multiple-choice questions that are worth 1
point each. You
will be allowed 3 hours to take the exam and you will be allowed to use a
graphing calculator.
Concepts and Objectives
The bulleted list and sample questions below may not refer to all the
material that will be in the
exam. This list only provides additional information for some of the student
expectations tested
in the Algebra 2 First Semester Credit by Exam. The use of problem-solving
skills is important;
all problem-solving activities require more than one step. In addition, you may
be asked to use
algebra and arithmetic skills from previous math courses. To prepare for this
exam, refer to the
Texas Essential Knowledge and Skills for Algebra 1, Geometry, and Algebra 2.
Ultimately, you should use the TEKS to guide your exam preparation.
In Algebra 2A, you learned about the foundations of
functions, including translations, dilations,
and transformations. You also learned about linear equations, linear
inequalities, systems of
linear equations, matrices, quadratic equations, square root equations, and
complex numbers. On
the exam, you should be able to
• identify linear, quadratic, or exponential functions
given words that describe a problem
situation, a table, a graph, or a function rule
• use words to describe linear, quadratic, or exponential functions given a
table, a graph, or a
function rule
• use the definition of slope to identify linear relationships
• make a table of values for linear, quadratic, or exponential function rules
given words that
describe a problem situation, a graph, or a function rule
• graph linear, quadratic, or exponential function rules given words that
describe a problem
situation, a table, or a function rule
• write linear, quadratic, or exponential function rules given words that
describe a problem
situation, a table, or a graph
• describe the domain and range of a linear, quadratic, square root, or
exponential function rule
• describe the meaning of the slope and y-intercept given a problem situation
• describe how changing the linear, quadratic, or exponential function rule
shifts the graph to
the left or right and up or down
• describe how changing the coefficient of the X^2 term impacts the graph of a quadratic
function
• use translations to the find a new coordinate of the y-intercept or the
highest point of the
graph
• use translations to identify a new function
• determine the translation applied to an original function that produced a new
function
• identify function rules that represent a reflection across the x-axis or
y-axis
• describe the meaning of the slope and y-intercept given a problem situation
• make predictions about data
• solve linear equations and inequalities using symbolic methods
• write a system of linear equations given a problem situation
• graph a system of two or three linear equations or inequalities
• solve systems of two or three linear equations by graphing, substitution, and
elimination
methods
• interpret the meaning of specific points that make a system of equations true
• add matrices
• multiply matrices
• write a matrix equation that represents a given problem situation
• show by finite differences that a table of data represents a quadratic
function
• write a quadratic function in vertex form
• identify the vertex, axis of symmetry, and the minimum or maximum value of a
quadratic
function
• describe the meaning of the vertex given a problem situation
• find and graph the inverse function for linear and quadratic functions
• rewrite functions by completing the square
• use the area formula for rectangles to write quadratic function rules and to
solve problem
situations
• determine the height of an object that is launched straight into the air given
the initial height
and initial velocity
• solve quadratic equations by using factoring, graphing, completing the square
and the
quadratic formula
• solve problem situations using the graph of a quadratic function
• solve quadratic inequalities by using graphing and symbolic methods
• solve square root equations by using graphing and symbolic methods
• determine the factors and zeros of an equation given the solutions or the
graph
• determine a possible quadratic equation given the zeros
• write a quadratic equation given the zeros and the coefficient of the X^2 term
• write a quadratic equation given the solutions and a point at through which
the graph passes
• determine the value of c given the coefficient of the X^2 and x terms and the minimum or maximum value of the quadratic function
• determine the characteristics of the discriminant given a quadratic function
rule or graph
• determine if a quadratic equation has one, two, or no solutions
• add, subtract, and multiply complex numbers
• determine the graphs of 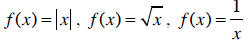
Sample Questions
These sample questions will give you a better idea of the types of questions you
can expect on
the Credit By Exam. These questions are provided to illustrate the format of the
exam; they are
not a duplicate of the actual exam. In order to be successful on the exam, you
must study and
review all of the concepts listed above.
Multiple-Choice
This part contains 5 multiple-choice questions. Circle the letter of the correct
response to each of
the following questions.
1. Solve the following system of equations.
2a + 3b + c = –2
a – b + 2c = 9
4a – 4b + 3c = 11
A (–1, –2, 6)
B (–4, 1, 3)
C (–2, –1, 5)
D (2, –3, 3)
2. What is the new rule if y = 3x + 6 is shifted left 4
units and up 3 units?
A y = 7x + 9
B y = 3x + 14
C y = 3(x + 4) + 9
D y = 4x + 3
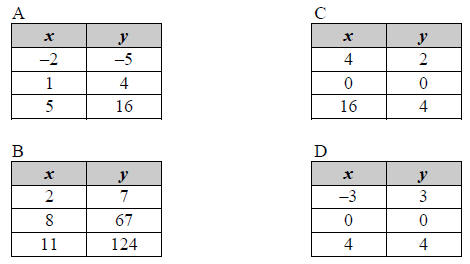
3. Which table of data represents a linear relationship?
4. What is the result when the two matrices are added together?

5. Which image is the graph of the function 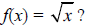
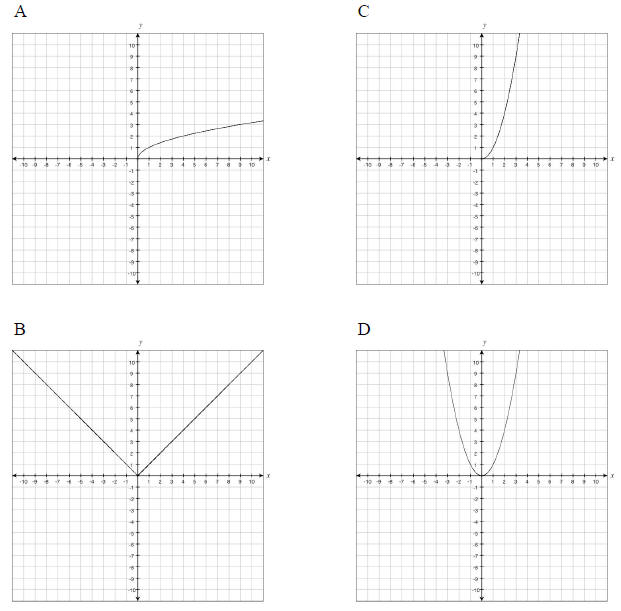
Answer Key
| Item Number | Correct Answer | TEKS |
| 1 | C | (b)(2A.3)(B) |
| 2 | C | (b)(2A.4)(B) |
| 3 | A | (b)(2A.1)(B) |
| 4 | A | (b)(2A.3)(B) |
| 5 | A | (b)(2A.4)(A) |


